16. Игры 2х2 и их решение.

Игра 2х2 – самая простая конечная игра, её матрица имеет вид табл. 3.2.

Если для этой матрицы α=β, то игра имеет седловую точку и её решение – это пара чистых стратегий, пересекающихся в седловой точке.

Если в этой матрице седловой точки нет и α≠β, то необходимо искать решение в смешанных стратегиях. Пара оптимальных смешанных стратегий: 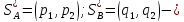и цена игры в этом случае определяется по формулам:

17. Геометрическая интерпретация решений игры 2х2.

Решение игры 2х2 допускает наглядную геометрическую ин­терпретацию.

Пусть игра задана платежной матрицей Р = (а_ij), i, j = 1, 2. По оси абсцисс отложим единичный отрезок А₁А₂; точка A₁ (x = 0) изображает стратегию А₁, а все промежуточ­ные точки этого отрезка —смешанные стратегии S_A первого иг­рока, причем расстояние от S_A до правого конца отрезка —это вероятностьр₁стратегииА₁, расстояние до левого конца —вероятность p₂ стратегии А₂. На перпендикулярных осях I—I и II—II откладываем выигрыши при стратегиях А₁ и А₂ соответственно. Если 2-й игрок примет стратегию В₁, то она дает выигрыши а₁₁ и а₂₁ на осях I—I и II—II, соответствующие стратегиям А₁ и А₂. Обозначим эти точки на осях I—I и II—II буквой В₁.Средний выигрыш v₁, соответствующий смешанной стратегии S_A, опреде­ляется по формуле математического ожидания v₁ = а₁₁р₁ + а₂₁р₂ и равен ординате точки М₁, которая лежит на отрезке В₁В₁ и имеет абсциссу S_A (рис. 1).

Рис. 1 Рис. 2

Аналогично строим отрезок В₂В₂, соответствующий примене­нию вторым игроком стратегии В₂ (рис. 2). При этом средний выигрыш v₂ = а₁₂р₁ + а₂₂р₂ — ордината точки М₂.

В соответствии с принципом минимакса оптимальная страте­гия S^*_A такова, что минимальный выигрыш игрока А (при наи­худшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 3), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B₁N —против стратегии В₁, на участке NB₂ —против стратегии B₂). Оптимальную стратегию S^*_A = (p^*₁, р^*₂) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v. На рис.3 обозначе­ны также верхняя и нижняя цены игры  и .

Применим геометрический метод для решения следующей за­дачи.

Рис. 3 Рис. 4

Пример. Решить графически игру, заданную платежной матрицей:

Решение. Откладываем по оси абсцисс (рис. 4) единичный отрезок А₁А₂. На вертикальной оси I—I откладываем отрезки: а₁₁ = 1,5, соответствующий стратегии В₁, и а₁₂ = 3, соответствующий стратегии В₂. На вертикальной оси II—II отрезок а₂₁ = 2 соответ­ствует стратегии В₁, отрезок а₂₂ = 1 соответствует стратегии В₂ (см. рис. 4). Нижняя цена игры =а₁₁ = 1,5. Верхняя цена игры  =а₂₁ = 2, седловая точка отсутствует. Из рис. 4 видно, что абсцисса точки N определяет оптимальную стратегию S^*_A, а орди­ната —цену игры v. Точка N является точкой пересечения прямых В₁В₁ и В₂В₂. Уравнение прямой В₁В₁, проходящей через точ­ки (0; 1,5) и (1;2):

Уравнение прямой В₂В₂, проходящей через точки (0; 3) и (1;1):

Точка пересечения прямых является решением системы:

- там знак системы, он не исправляется

или х = 0,6; у = 1,8, т. е. N (0,6; 1,8).

Таким образом, р^*₁ = 0,6, р^*₂ = 1 — 0,6 = 0,4; оптимальная стратегия S^*_A = (0,6; 0,4), цена игры v = 1,8.

­Геометрически мо­жно также определить оптимальную страте­гию игрока В, если поменять местами иг­роков А и В и вместо максимума нижней границы А₂МА₁ в соот­ветствии с принципом минимакса (рис. 5) рассмотреть минимум верхней границы.

Рис. 5

Абсцисса точки М определяет q^*₂в оптимальной стратегии игрока В, ордината этой точки —цена игры. Прямая А₁А₁, проходящая через точки (0; 1,5) и (1; 3), удовлетворяет уравнению

Прямая А₂А₂, проходящая через точки (0; 2) и (1; 1), удовле­творяет уравнению у =—х +2.

Координаты их точки пересечения М —это решение системы уравнений:

откуда х = 0,2; у = 1,8, т. е. q^*₂ = 0,2, q^*₁ = 1— q^*₂ = 0,8, х =у = 1,8, S^*_B = (0,8; 0,2).

Оптимальное решение игры найдено.

Из решения задачи следует, что геометрически можно оп­ределять оптимальную стратегию как игрока А, так и игрока B, в обоих случаях используется принцип минимакса, но во втором случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум. Если платежная мат­рица содержит отрицательные числа, то для графического решения задачи лучше перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение игры при этом не изменится, а цена игры увеличится на это число. В примере выше платежная матрица не имела седловой точки ().

При наличии седловой точки графическое решение дают вариан­ты, изображенные на рис. 6 и 7. На рис. 6 наибольшей орди­натой на ломаной B₁NB₂ обладает точка B₂, поэтому оптимальной является чистая стратегия А₂ для игрока А (В₂ —для игрока В), т.е. оптимальное решение: S^*_A = (0; 1), S^*_B = (0; 1). Игра имеет седловую точкуа₂₂ = v.

Рис. 6 Рис. 7

Чистая стратегия В₂ (рис. 7) не выгодна для игрока В, по­скольку при любой стратегии игрока А она дает последнему больший выигрыш, чем чистая стратегия В₁. На основании принципа минимакса выделим прямую В₁В₁ и на ней точку В₁ с наибольшей ординатой на оси I—I. Чистая стратегияА₂является оптимальной для игрока А, а чистая стратегия В₁ —для игрока В.

Оптимальное решение: S^*_A = (0;1), S^*_B = (1;0), цена игры v=а₂₁= =, т.е. имеется седловая точка.