19. Решение игр mx2

В игре mx2 мы имеем две m стратегий (A1, A2, …, Аm), а наш противник 2 стратегии (B1, B2). В игре mx2 всегда имеется решение, содержащее не более двух активных стратегий у каждого из игроков, если эти активные стратегии игроков будут найдены, то игры mx2 превращаются в игры 2x2 (описано в вопросе 18).

Правила решения игр mx2:

1. строится графическое изображение игры;

2. выделяется верхняя граница выигрыша, и на ней находится точка оптимума с наибольшей ординатой;

3. определяется пара стратегий, пересекающихся в точке оптимума M. Эти стратегии являются активными стратегиями игрока B. Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них;

4. решается полученная игра 2x2.

Пример:

Дана матрица стратегий

Решение:

	B1	B2	αi
A1	0,4	1,0	0,4
A2	0,5	0,5	0,5
A3	1,0	0,3	0,3
A4	0,8	0,3	0,3
βj	1,0	1,0

α= 0,5, β= 1,0. Седловой точки нет.

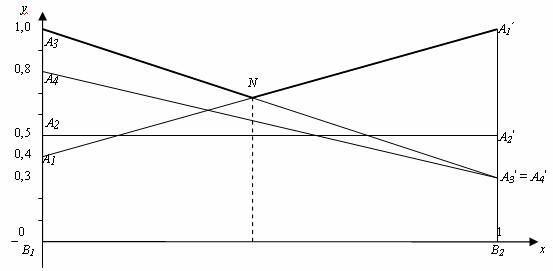
1. Cтроим графическое изображение игры относительно игрока В.

Если А применяет А1, то при использовании игроком В стратегии В1 выигрыш игрока А равен 0,4, а выигрыш А при стратегии В2 равен 1,0, поэтому на перпендикулярах строим такие отрезки. Видно, что стратегия А4 заведомо невыгодная по сравнению со стратегией А3 (выигрыш меньше).

2. Выделяем верхнюю границу выигрыша А3NА1′; точка с наименьшей ординатой – N.

3. В этой точке пересекаются отрезки А1А1′ и А3А3′, соответствующие активным стратегиям А1 и А3. Стратегия А2 не является активной, поэтому из матрицы исключаем вторую и четвертую строки:

4. решаем игру:

13p3 = 6; p3 = 6/13; p1 = 7/13

q2 = 6/13.

Ответ: γ = 44/65; PA = (7/13; 0; 6/13; 0); QB = (7/13; 6/13).

(γ – стоимость игры)

Примечание: Игроку А не выгодно отклоняться от спектра своих активных стратегий.

20. Решение игр mxn.

Для игр m × n геометрическая интерпретация неприменима. Здесь применяются чисто расчетные методы. Можно показать, что решение любой конечной игры m × n может быть сведено к задаче линейного программирования.

Рассмотрим игру m × n. У игрока A имеется m стратегий: A₁, A₂, ..., A_m; у игрока B есть n стратегий: B₁, B₂, ..., B_n. Такая игра задается матрицей игры m × n [a_ij]. Нужно найти две оптимальные смешанные стратегии S*_A = (p₁, p₂, ..., p_m) и S*_B = (q₁, q₂, ..., q_n), где p₁, p₂, ..., p_m и q₁, q₂, ..., q_n – вероятности применения соответствующих чистых стратегий A₁, A₂, ..., A_m и B₁, B₂, ..., B_n и , .

Нахождение S^*_A. Положим, что цена игры γ положительна, γ ≥ 0. Это всегда можно сделать, добавив ко всем членам матрицы игры достаточно большое положительное число М. При этом решение игры не изменится, а найденную величину γ нужно будет в конце также увеличить на М.

Если мы применяем S^*_A, а противник – чистую стратегию B _j, то наш средний выигрыш будет равен

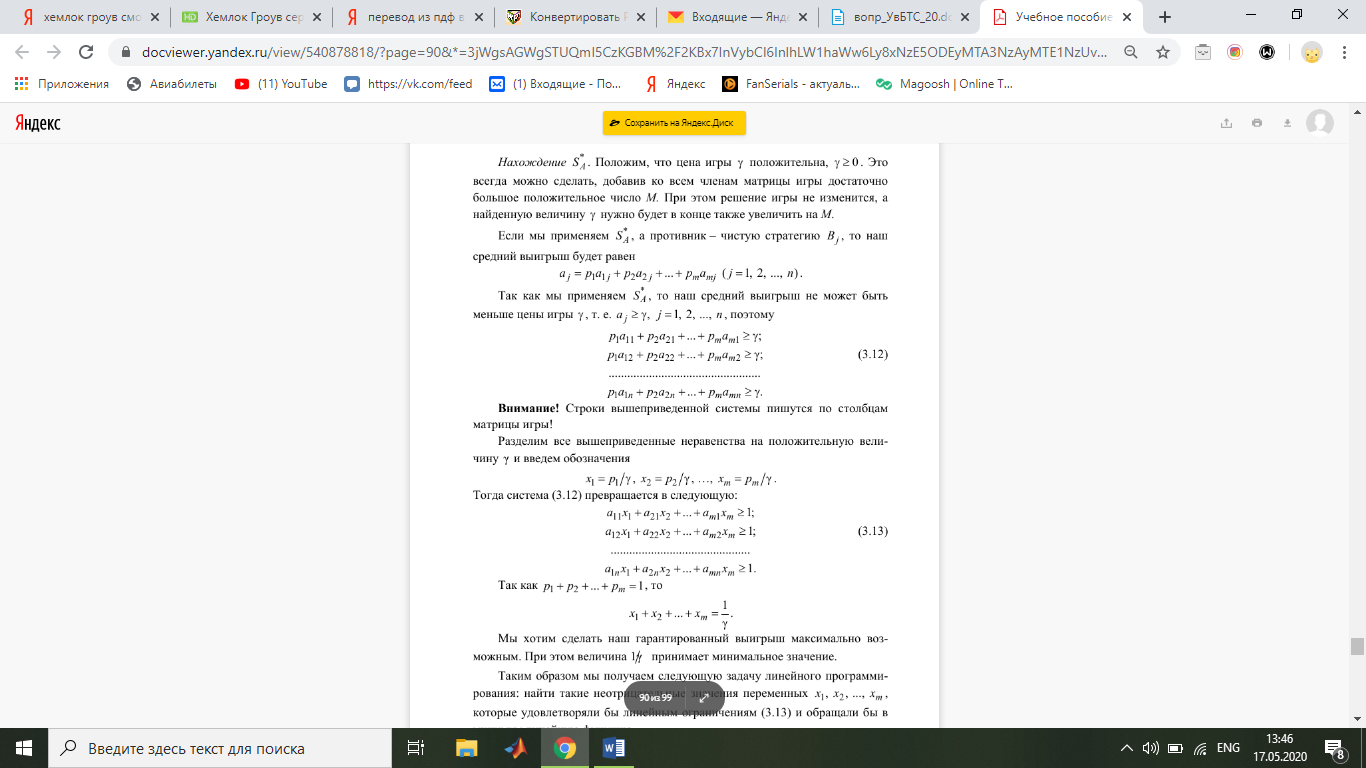
Так как мы применяем S^*_A, то наш средний выигрыш не может быть меньше цены игры γ, т. е. a _j ≥ γ, j = 1, 2, ..., n, поэтому

(1)

Строки вышеприведенной системы пишутся по столбцам матрицы игры.

Разделим все вышеприведенные неравенства на положительную величину γ и введем обозначения

Тогда система (1) превращается в следующую:

(2)

Так как p₁ + p₂ + ... + p_m = 1, то

Мы хотим сделать наш гарантированный выигрыш максимально возможным. При этом величина 1/ γ принимает минимальное значение.

Таким образом мы получаем следующую задачу линейного программирования: найти такие неотрицательные значения переменных x₁, x₂, ..., x_m, которые удовлетворяли бы линейным ограничениям (2) и обращали бы в минимум линейную функцию

Решив эту задачу линейного программирования, мы можем найти оптимальную стратегию S^*_A игрока A.

Нахождение S_B^*. Оптимальная стратегия S_B^* находится аналогично. Разница заключается в том, что игрок B стремится не максимизировать, а минимизировать выигрыш, а значит максимизировать величину 1γ. Следовательно, вместо условий (2) должны соблюдаться условия

(3)

Требуется так выбрать неотрицательные значения переменных y₁, y ₂, ..., y_n, чтобы они удовлетворяли условиям (3.14) и обращали в максимум линейную функцию

L = y₁ + y ₂ + ... + y_n = 1γ

или, что то же самое, обращали в минимум линейную функцию L′ = −L:

L ′ = − y₁ − y ₂ − ... − y_n = − 1γ.

Таким образом, любая конечная игра m × n сводится к паре задач линейного программирования.