13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.

Рассмотрим игру (модель конфликтной ситуации), в которой участвуют два игрока A и B, имеющие прямо противоположные интересы, поэтому выигрыш одного равен проигрышу другого. Такая игра называется парной игрой с нулевой суммой. Если игрок A выигрывает a, то игрок B при этом выигрывает -a, поэтому сумма выигрышей всегда равна нулю. Процесс игры заключается в последовательных ходах (личных – сознательных и случайных) противников, а совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации называется стратегией игрока. При конечном числе стратегий игра будет конечной. Пусть у игрока A имеется m возможных стратегий A₁, A₂, …, A_m, а у игрока B – n возможных стратегий B₁, B₂, …, B_n. Пусть также известны величины a_ij – выигрыши игрока A при использовании A_i с его стороны и B_j со стороны противника. Тогда игра, называемая игрой m × n, может быть представлена таблицей, называемой платежной матрицей или просто матрицей игры.

Платежная матрица (матрица игры)

Приведение игры к матричной форме может само по себе составить трудную задачу, однако таким путем многоходовая игра фактически сводится к одноходовой – от игрока требуется сделать только один ход: выбрать подходящую стратегию. Для данного игрока среди всех стратегий имеется оптимальная, обеспечивающая ему максимальный выигрыш. Задача теории игр – нахождение оптимальных стратегий игроков в предположении одинаковой «разумности» противников.

14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.

Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый игрок стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, тогда как второй игрок выбирает стратегию, приводящую его к минимальному проигрышу. В этой связи вводят понятия нижней и верхней чистой цены игры.

По матрице игры определяются нижняя и верхняя цены игры.

Пусть , , тогда

Нижней чистой ценой игры (максимином) называется число, определяемое по формуле:

Верхней чистой ценой игры (минимаксом) называется число, определяемое по формуле:

Принцип минимакса:

Принцип выбора противниками стратегий, соответствующих получению ими выигрышей и .

Принцип осторожности, заставляющий игроков придерживаться максиминной и минимаксной стратегий соответственно, а минимаксную стратегию и максиминную стратегию называют общим термином «Минимаксные стратегии»

Известно, что минимаксные стратегии устойчивы по отношению к информации о поведении другой стороны только в случае, если . В этом случае матрица игры имеет седловую точку, а величина 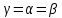называется ценой игры.

Оптимальные чистые стратегии – стратегии и , при которых достигается выигрыш . Совокупность этих стратегий – решение игры

(Иными словами: Целью участников любой матричной игры является выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В минимальный проигрыш.

Определение. Чистую стратегию Ai игрока А называют оптимальной, если при ее применении выигрыш игрока А не уменьшается, какими бы своими стратегиями не пользовался игрок В. Оптимальной для игрока В называют чистую стратегию Bj, при использовании которой проигрыш игрока В не увеличивается, какие бы стратегии не применял игрок А.)

Пример 1 — Самая простая конечная игра – игра . Ее матрица имеет вид таблицы. Если для этой матрицы , то игра имеет седловую точку и ее решение – это пара чистых стратегий, пересекающихся в седловой точке.

Пример 2 — Найти нижнюю и верхнюю цены игры с платежной матрицей

В каждой строке платежной матрицы найдем наименьший элемент и запишем его справа от матрицы. В каждом столбце платежной матрицы найдем наибольший элемент, и запишем его снизу от матрицы. В результате получим таблицу

Нижняя цена игры

Верхняя цена игры

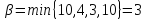
, цена игры =3