
GOSy_po_vsemu_vnutr
.pdf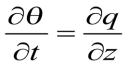
между |
полураспа |
и от |
от свойств |
|
порядка)в-во при |
зонами |
да |
свойств |
вещества |
|
движ. в структ. |
поров. |
|
вещества |
|
|
почве |
простр. |
|
|
|
|
|
|
|
|
|
|
|
Модели переноса вещества в почвах основаны на ковективно-диффузионном уравнении, модели солепереноса, модель FAUST. Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Конвективный перенос dc/dt=v*dc/dz, где v=qw/ε, где qw-макроскопическая скорость потока по Дарси.
Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Например если рассмотреть
абстрактную микропору и введем мигрант, то он будет двигаться вместе с основным движущимся составом (водой). Уравнение неразрывности для воды
Изменение влажности определенной толщи почвы во времени пропорционально изменению потока влаги в рассматриваемой толще колонки. В случае с солепереносом изменение концентрации солей во времени пропорционально изменению потока солей в рассматриваемой толще колонки и уравнение выглядит ∂c/∂t = ∂qc/∂z
При движении растворенных веществ в пористых средах, таких как почва, наблюдаются следующие явления:
1.нет четкой границы между поступающим раствором и почвенной влагой, происходит «размыв» фронта движущегося раствора;
2.при движении происходит непрерывное перемешивание раствора и почвенной влаги, в результате образуется расширяющаяся зона дисперсии (зона смешивания, переходная зона, шаг смешения);
3.интенсивность изменения концентрации индикатора больше в направлении
движения потока по сравнению с направлением, перпендикулярным движению; 4. явление перемешивания, или «размыва», фронта движущегося раствора
тем сильнее, чем выше скорость потока и значительнее дифференциация размеров пор.
Около стенки твердой фазы образуется так называемая зона выталкивания аниона, или нерастворяющий для аниона объем пристеночной почвенной влаги. Наличие такого нерастворяющего объема приводит к более быстрому появлению аниона, и пик выходной кривой будет приходиться на значение такта, меньшее единицы.
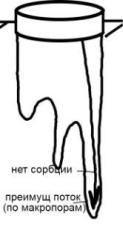
Явление приемущественных потоков
Параметры переноса солей: D*-гидродин диффузия, θ*-влажность нерастворяющего объема (при движении анионов), Ксорбции – константа распрделения (при движ сорбирующихся в-в), к0,к1,к2 – константы равновесия.
MACRO, PEARL, PELMO.Основную роль в транспорте пестицидов в окружающей среде играет вода и поэтому, модели предполагают использование в качестве одних из входных параметров гидрофизические свойства почв, от которых во многом зависит точность прогноза поведения пестицидов в почвах. Настраивая гидрофизический блок моделей, можно добиться более адекватного прогноза, учитывающего региональную специфику почв.
Сравнение прогнозной и экспериментальной динамики содержания имидаклоприда в почвах показало, что в целом модели идентично предсказывали остаточные количества инсектицида в почвенной толще. Однако модель MACRO количественно более точно прогнозировала профильное распределение имидаклоприда и его попадание в
лизиметрические воды.
Модель PELMO. Состоит из отдельных блоков: почва, вещество( учитываются константы кинетики К0,К1,К2), растения и метеоусловия. Учитывается количество и свойства слоев (ОГХ, Кр).
Назад

39. Модели переноса влаги в почвах. Уравнение Ричардса. Возможность решения уравнения, введение дифференциальной влагоемкости.
Уравнение Ричардса, описывающее влагоперенос в зоне аэрации (в ненасыщенной зоне), было сформулировано Лоренцо А. Ричардсом в 1931 году. Оно представляет собой нелинейное дифференциальное уравнение в частных производных, основная трудность решения которого заключается в отсутствии точных аналитических решений.
Закон Дарси разработан для описания потока влаги в водонасыщенной пористой среде, адаптируя его, Ричардс использовал предложение Букингема и вывел общее дифференциальное уравнение в
частных производных, которое описывает ненасыщенный влагоперенос в зоне аэрации. Наиболее известной формой записи является:
Уравнение Ричардса аналогично уравнению влагопереноса в насыщенной зоне, переход от одного к другому обусловлен представлением напора в виде h = ψ + z, и заменой насыщенного потока ненасыщенным. Использование формы записи приведенной выше обусловлено удобством описания граничных условий (часто описываемых в терминах напора, например для использования атмосферного условия ψ = 0).
Красивый вывод уравнения из уравнения Дарси

или в чуть иной записи:
Нетрудно заметить, что в этом уравнении две переменные влажность ( θ ) и давление влаги (Рк с). Решения его даже специальными методами невозможно. Надо привести уравнение к одной переменной. Для этого вводят понятие дифференциальной влагоемкости см последн. формулу. Эту величину используют, экспериментально или другими способами получая основную гидрофизическую характеристику ОГХ («кривая водоудерживания», «water retention curve») – зависимость объемной влажности почв от капиллярно сорбционного давления.
Назад
40. Модели переноса тепла в почве. Основное уравнение теплопереноса.
Поток тепла в почве описывается законом Фурье, который связывает поток с градиентом температуры через коэффициент пропорциональности –
теплопроводность, λT:  где qT – поток тепла в почве
где qT – поток тепла в почве
[кал/см2∙сут], λT – коэффициент теплопроводности [кал/см °С сут или Дж/см∙°С, либо Вт/м∙К], который равен количеству тепла (в кал или Дж), прошедшего в единицу времени (сут или секунду) через единичное сечение почвы (см2 или м2) при единичной толщине слоя почвы (1 см или 1 м) и при разнице температур в 1 °С (или 1 °К). [кал/см∙С°∙сут], ∂T/∂z – градиент температуры [°С/см]. Здесь следует отметить, что речь идет об установившемся, стационарном потоке тепла в почве, как и в случае с уравнением Дарси. Только для этих условий справедливо уравнение Фурье. Основным теплофизическим свойством, как следует из этого уравнения, является параметр
теплопроводности – коэффициент теплопроводности.
В почве, как известно, перенос тепла происходит по четырем основным механизмам: (1) кондукция – перенос тепла при непосредственном контакте частиц друг с другом; (2) конвекция – прогревание за счет струйчатого перемешивания жидкой и газообразной фаз; (3) перенос «скрытой теплоты» (теплопароперенос) – перенос тепла совместно с парами воды, образующимися (с потерей тепла) в одной малой области почвы и конденсирующимися (с выделением тепла) в другой и (4) прямого инфракрасного излучения. Механизм переноса тепла и соответственно теплопроводность зависит от величины влажности почвы. В сухой почве, теплоперенос будет обусловлен лишь отдельными немногочисленными контактами (кондукция). По мере образования водной
пленки, частицы приближаются друг к другу, но имеется и свободное поровое пространство (кондукция и пароперенос). При дальнейшем увеличении влажности теплопроводность будет возрастать уже слабо, в основном за счет свободной циркуляции жидкости (конвекция). Максимальная теплопроводность обычно наблюдается при влажности в диапазоне влажность разрыва капиляров −
наименьшая |
влагоемкость |
(ВРК НВ). |
Поэтому |
и |
зависимость |
коэффициента |
теплопроводности |
от |
|
влажности носит характер, близкий к экспоненциальному, когда в диапазоне ВРК НВ, кривая выполаживается, приближаясь к максимальным значениям. Таким образом, она имеет вид близкий к логарифмической или сигмоидной функции в зависимости физических особенностей почв
Назад
41 Педотрансферные функции.
Педотрансферными функциями (ПТФ) называют зависимости, позволяющие восстанавливать основные гидрофизические функции почв - прежде всего основную гидрофизическую характеристику (ОГХ – зависимость между капиллярно-сорбционным давлением влаги и влажностью) – по традиционным, известным из материалов Почвенных служб или традиционно определяемым базовым свойствам почв.
Методы определения ПТФ:
1. Точечный.Основан на представлении о капиллярном строении порового пространства как образующегося между почвенными частицами, радиусы которых известны из данных по гранулометрическому составу. Форма и размеры частиц диктуют способ упаковки, а для каждого способа упаковки существует своя геометрическая модель порового пространства. Можно для каждого типа упаковки определить распределение диаметров капилляров, а диаметр напрямую связан с капиллярно-сорбционным давлением. Этот путь получения ОГХ не всегда дает хорошие результаты: простые геометрические представления об упаковке частиц далеко не всегда применимы к почве с ее особенностями порового пространства, образованного агрегатами различного порядка, биопорами, трещинами и другими специфическими почвенными образованиями.
2. Регрессионные уравнения связывающие равновесные значения
«давление-влажность» Используя многочисленные экспериментальные данные по базовым свойствам почв и ОГХ, методом наименьших квадратов находят эмпирические коэффициенты a,b,c,d,e,f в уравнении, например, такого вида:
где i относится к одной из равновесных точек pF-θ на ОГХ, а ω - доля соответствующей фракции в гранулометрическом составе почвы по международной классификации, ωС – содержание органического вещества, ρb – плотность почвы
. Необходимые правила:
1. большой массив данных по ОГХ и по физическим свойствам почв. Чем этот массив больше, тем достовернее получается ПТФ определения ОГХ. 2.Наиболее надежные ПТФ получаются, если исходные данные систематизированы для конкретного района, почвенного типа (подтипа, рода, который в основном определяет гранулометрический состав), горизонта, структуры и текстуры (группировка по гранулометрическому составу). Этот принцип носит название «предварительной группировки», соблюдение которого необходимо. При таком подходе удается достичь величины средней квадратической ошибки определения влажности до 0.07-0.02 см3/см3 при давлениях влаги -330...-15000 см водн. ст.
3.регрессионные уравнения, связывающие параметры аппроксимации ОГХ с традиционными физическими свойствами.
Получают выражения для параметров уравнения ван Генухтена (n - крутизна наклона, α - обратное от давления воды (1/Pb), θs - влажность насыщения < порозности (ε), θr - остаточная влажность) от фундаментальных свойств почвы.
(Qi-Qr)/(Qs-Qr) =Se = {1/(1+α|pn|)}m
где m = 1 - 1/n
- уравнение ван Генухтена для описания ОГХ
Этот подход основан на том, что ОГХ удается описать плавной функцией, т.е. аппроксимировать математическим уравнением. Если выбран вид функции для аппроксимации, то в этой функции всегда есть некоторые параметры - коэффициенты, степени или свободные члены выбранной функции. Так, для ОГХ одного почвенного образца эти параметры получают при аппроксимации конкретное числовое значение. Если возьмем ОГХ для другого почвенного образца, то после аппроксимации той же самой функцией возникнут несколько иные числовые значения параметров.
4. Метод «нейронных сетей». Называется так из за узла в котором происходит решение, то есть процедура статистического анализа.Перебор св-в и выбор наиболее информативных, установление связи. Итоговое уравнение тоже регрессионного типа, но перебором св-в и с выделением самых значимых факторов, работает лучше чем пошаговая регрессия.
Назад
