
полезная метода
.pdf
уравнение:
225+ 0,2.Х = 0,5.(250 + Х); Х = 333,3 г
4.Сколько Н2О необходимо прибавить к 200 мл 20% р-ра Н2SO4 (ρ=1,14), чтобы получить 5% р-р?
Дано: Vр
(Н2SO4)=200мл ρ=1,14г/мл ω1=20% ω2=5%
m(Н2О)=?
1 способ.
mр1(Н2SO4)= V*ρ=200*1,14=228(г)
mв-ва= mв ва *100% 45,6*100% 912г2 % 5%
m(Н2О)доп= mр-ра2 – mр-ра1=912 – 288=684г.
2 способ.
20% 0% 5%
228*20 + х*0 = (228 + х)*5
4560 = 1140 + 5х
5х =3420 х = 684
3 способ. Диагональная схема («правило креста»)
В точке пересечения двух прямых обозначают концентрацию смеси, у концов этих прямых по левую сторону от точки пересечения указывают концентрации составных частей смеси, а по другую – разности концентраций смеси и её составных частей.
20% |
5частей – это 228 г |
|
5% |
0% |
15частей – это х г |
m(Н2О)=228:5*15=684г
Ответ: масса воды 684 г.
5. Вычисления с использованием молярной концентрации эквивалента.
Определите концентрацию раствора КОН, если на нейтрализацию 0,035 л 0,3н H3PO4 израсходовано 0,02 л раствора КОН.
Решение.
Из закона эквивалентов следует, что количество эквивалентов всех участвующих в химической реакции веществ одинаково. В реакции участвуют 0,035.3 = 0,0105 эквивалента Н3РО4.
Для нейтрализации Н3РО4 потребуется такое же количество вещества эквивалента КОН, т.е.
V(H3PO4) . CN(H3PO4) = V(KOH) . CN(KOH)
21

VH3PO4 CN,H3PO4 0.0105 0.53H VKOH 0.02
Ответ: нормальность раствора КОН 0,53 н
§4. Задачи для самостоятельного решения
1.При хроническом гастрите язвенной болезни желудка иногда назначают в качестве противовоспалительного средства внутрь 0.05 % раствор AgNO3 по 15 мл. Какая масса ионов серебра содержится в дозе объемом 15 мл (р = 1г/мл).
2.При отравлениях белым фосфором, принятым внутрь, назначают 0.5г сульфата меди в 100 г теплой воды. Какую массу (г) медного купороса необходимо взять, чтобы массовая для сульфата меди была равна 0.5%?
3.При взаимодействии 0,91 г некоторого металла с раствором соляной кислоты выделилось 0,314 л водорода. Чему равна атомная масса металла?
4.Найдите молярную концентрацию 30%-ной серной кислоты (плотность раствора 1,22 г/мл).
5.В больнице для промывания слизистых оболочек пациенту назначили 0.5%-ный раствор перманганата калия, а в наличии оказался только 6%-ный раствор этого вещества. Сколько воды и 6%-ного раствора (р = 1.01 г/мл) потребуется для приготовления 1 л 0.5%-ного раствора перманганата калия?
6.В медицинской практике для промывания ран применяют 0.5%-ный раствор перманганата калия (р = 1 г/мл). Какой объем раствора можно приготовить из 10 г перманганата калия?
7.В лаборатории имеется раствор с массовой долей гидроксида натрия 30%, плотность которого 1,33 г/мл. Какой объем этого раствора надо взять для приготовления раствора объемом 250 мл с массовой долей гидроксида натрия 14: и плотностью 1,15 г/мл?
8.Как приготовить 300 г 15%ного раствора смешиванием 5%- ного и 30%-ного?
9.Определите массовую долю (%) хлорида калия в растворе, содержащем 0,053 кг KCl в 0,5 л раствора, плотность которого 1,063 г/мл. Ответ: 10%.
10.Какова масса NaOH, содержащегося в 0,2л раствора, если молярная концентрация раствора 0,2 моль/л? Ответ: 1,6 г.
11.Определите молярную концентрацию эквивалента хлорида железа (III), если в 0,3 л раствора содержится 32,44 г FeCl3. Ответ: 2 моль/л.
22
12.В какой массе эфира надо растворить 3,04 г анилина C6H5NH2, чтобы получить раствор, моляльность которого 0,3 моль/кг? Ответ: 0,107 кг.
13.Определите титр 0,01N КОН. Ответ: 0,000561 г/мл
14.Рассчитайте молярные доли глюкозы С6Н12О6 и воды в растворе с массовой долей глюкозы 36%. Ответ: 0,053; 0,947.
15.Определите массовую долю (в%) хлорида Na в растворе, если в
500г H2O растворено 125г соли. |
(20%) |
16.В 1 л воды растворено 2 моль NaOН. Определите ω% NaOН в растворе. (7,4%)
17.Определите ω% NН3 в растворе, полученном при растворении
112л NН3(н.у) в 315 мл H2O. |
(21,2%) |
18.Сколько граммов НNO3 содержится в 200 мл 40% раствора плотностью 1250 кг/м3? (160г)
19.Определите ω% Cа(NO3)2 в растворе, полученном при смешивании 300г 10% раствора и 500г 20% раствора Cа(NO3)2. (16,25%)
20.К 300 мл 40% р-ра НNO3 ((ρ=1250 кг/м3) прилили 125 мл H2O.
Определите ω% НNO3 в полученном растворе. |
(30%) |
21.Сколько граммов хлорида К содержится в 750 мл 10% р-ра
(ρ=1,063 г/мл)? (79,7г)
22.Сколько граммов йода и спирта надо взять для приготовления
500г 5% йодной настойки? (25г I2; 475г C2H5OH)
23.Сколько граммов медного купороса нужно взять, чтобы
приготовить 5л 8% раствора CuSO4 (ρ=1,084 г/мл)? |
(678,3г) |
24.Сколько граммов 20% едкого натра надо добавить к 0,5 л воды,
чтобы получить 5% раствор? |
(166,7г) |
25.Сколько миллилитров H2O надо добавить к 500г 25% р-ра
вещества, чтобы получить 10% раствор? |
(750мл) |
26.Какой объем 15% р-ра NaOH (ρ=1,16 г/мл) можно приготовить
из 2 л 33% раствора (ρ=1,36 г/мл)? |
(5,16л) |
27.Сколько граммов KCl нужно растворить в 450г 15% раствора
KCl, чтобы получить 25% раствор? |
(60г) |
28.Какие объемы 60% Н2SO4 (ρ=1,1 г/мл) второй раствор нужно смешать, чтобы получить 10л 27% раствора (ρ=1,2 г/мл)? (2,25л; 7,75л)
29.Сколько воды необходимо прибавить к 500 мл 20% раствора
NaCl (ρ=1,152 г/мл), чтобы получить 4,5% раствор? |
(1988г) |
30.К 950 г H2O прибавить 50мл 48% раствора Н2SO4 (ρ=1,38 г/мл). вычислите процентное содержание Н2SO4 в полученном растворе. (3,25%)
31.Какой объем раствора Н2SO4 (ρ=1,8 г/мл) с массовой долей88% надо взять для приготовления раствора кислоты объемом 300мл и
плотностью 1,3г/мл с массовой долей Н2SO4 40%? |
(98,5мл) |
23
32. К раствору Н2SO4 |
объемом 400мл (ρ=1,1г/мл) и ω%=15% |
добавили воду массой 60г. Определить массовую долю Н2SO4 в |
|
полученном растворе. |
(13,2%) |
33.В лаборатории имеется раствор с массовой долей NaOH 30% (ρ=1,33 г/мл). Какой объем этого раствора надо взять для приготовления раствора объемом 250мл с массовой долей NaOH 14% (ρ=1,15 г/мл)? (100,9мл)
34.К раствору массой 250г, массовая доля соли в котором составляет 10%, прилили воду объемом 150мл. Определить ω% соли в
полученном растворе. |
(6,25%) |
35.В H2O объемом 200мл растворили образец соли, получив раствор с ω%=20%. К этому раствору еще добавили H2O объемом 150мл. Определить ω% соли в полученном растворе. (12,5%)
36.Какую массу раствора карбоната К с ω%=40% надо прибавить
к воде массой 500г для получения 15% раствора К2CO3? |
(300г) |
37.Какую массу 20% раствора NaCl необходимо добавить к воде
объемом 40мл для получения 6% раствора NaCl? |
(17,1) |
38.Через 1 л раствора NН3 с массовой долей 10% (ρ=0,96 г/мл), пропустили 10л NН3(н.у). Вычислить ω% NН3 в образовавшемся растворе. (16,6%)
39.В 1000 граммах воды растворили 219г кристаллогидрата CaCl2·6H2O. Определите массовую долю хлорида Са в полученном
растворе. (9,1%)
40. Кристаллогидрат CоCl2·6H2O массой 476 растворили в H2O. При этом получился раствор с массовой долей CоCl2 13,15%. Определить
массу воды, которая пошла на растворение. |
(1501г) |
41.Сколько кристаллогидрата FeSO4·7H2O необходимо взять,
чтобы приготовить 10кг. 5% раствора FeSO4? |
(914г) |
§5. Лабораторная работа «Приготовление раствора медного купороса»
Работа 1. Приготовление 0,5н раствора СuSO4 из СuSO4 5Н2О
1.Вычислите, какое количество СuSO4 5Н2О необходимо для приготовления 250 мл 0,5н раствора, рассчитанного на безводную соль.
2.Взвесьте это количество соли в предварительно взвешенное часовое стекло.
3.Высыпьте навеску через воронку в мерную колбу на 250 мл и тщательно смойте из промывалки часовое стекло над воронкой. Воронку также тщательно обмойте из промывалки дистиллированной водой.
4.Навеску растворите в небольшом количестве воды, затем долейте колбу до черты, закройте пробкой и хорошенько перемешайте.
24
5.Определите ареометром с помощью руководителя плотность полученного раствора.
6.Рассчитайте:
а) массовую долю (%) СuSO4 в приготовленном растворе; б) молярность полученного раствора.
7. Результаты опыта сведите в таблицу:
№ |
Вид определения |
Данны |
|
|
е |
|
|
опыта |
1 |
Объем заданного раствора |
|
2 |
Нормальность заданного раствора |
|
3 |
Весовое количество СuSO4 для приготовления |
|
|
заданного раствора |
|
4 |
Весовое количество СuSO4 5Н2О для приготовления |
|
|
заданного раствора |
|
5 |
Плотность заданного раствора из опыта |
|
6 |
Плотность раствора по таблице |
|
7 |
Массовая доля СuSO4 в заданном растворе |
|
8 |
Молярность заданного раствора |
|
Работа 2. Разбавление 0,5н раствора сульфата меди до 0,1н раствора.
1.Рассчитайте, сколько воды нужно прилить к 50мл полученного раствора для разбавления его до 0,1н.
2.Ополосните бюретку на 50мл небольшим количеством приготовленного раствора и наполните ее последним.
3.Вылейте 50мл полученного раствора в коническую колбу и разбавьте его вычисленным вами количеством воды, отмерив последнюю с помощью бюретки.
4.Дайте для проверки разбавленный раствор преподавателю.
5.Рассчитайте молярность разбавленного раствора.
6.Полученные данные сведите в таблицу:
№ |
Вид определения |
Данные |
|
|
опыта |
1 |
Объем 0,5н раствора СuSO4 , взятого для разбавления |
|
2 |
Объем воды, прибавленный для разбавления |
|
3 |
Плотность разбавленного раствора из опыта |
|
4 |
Плотность раствора по таблице |
|
5 |
Молярность разбавленного раствора |
|
7. Сделайте рисунки: мерной колбы ( рисунок должен показать правила отсчета), ареометра (как показано).
25
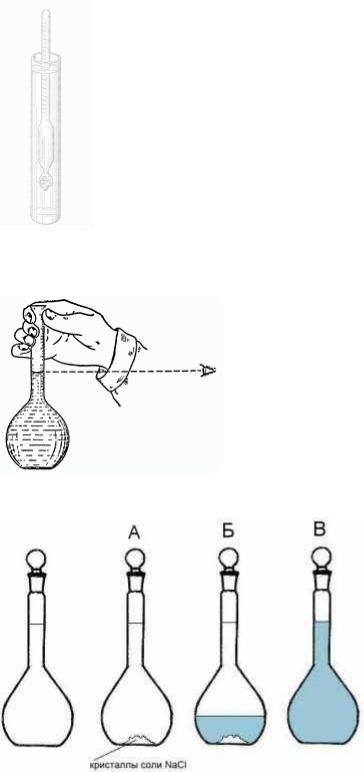
Рис.1 ареометр
Рис 2.Уровень жидкости
Рис 3. Приготовление раствора
26
ТЕМА 3.ЭНЕРГЕТИКА ХИМИЧЕСКИХ ПРОЦЕССОВ
Вопросы к занятию
1.Основные понятия Термодинамики: система (открытая, закрытая, изолированная, гомогенная, гетерогенная), внутренняя энергия, теплота, работа.
2.Первый закон термодинамики. Энтальпия.
3.Сформулируйте закон Гесса и следствия из него. Калорийность.
4.Второй закон термодинамики. Энтропия как критерий направления процесса. Факторы влияющие на величину энтропии
5.Третий закон Термодинамики.
6.Термодинамические функции: энергия Гиббса, энергия Гельмгольца
§1. Основные понятия термодинамики
Термодинамика изучает законы, которые описывают энергетические превращения, сопровождающие физические, химические и биологические процессы.
Процесс – это переход системы из одного состояния в другое, сопровождающийся необратимым или обратимым изменением хотя бы одного параметра, характеризующего данную систему.
Термодинамика изучает все объекты, рассматривая их особой структурой, называемой системой.
Системой называют тело или группу взаимодействующих тел, фактически или мысленно выделяемых из окружающей среды. Исходя из характера взаимодействия различных систем с окружающей средой, их подразделяют на открытые, закрытые и изолированные системы.
Открытая система обменивается с окружающей средой энергией и веществом.
Закрытой называют систему, в которой отсутствует обмен вещества с окружающей средой, но она может обмениваться с ней энергией.
Изолированная система характеризуется отсутствием обмена энергией и веществом с окружающей средой.
Понятие изолированная система является идеальным (абстрактным), так как на практике не существует материала, который абсолютно не проводил бы теплоту. Таким образом, абсолютно изолированных систем в природе нет.
Система может быть гомогенной (однородной) или гетерогенной (неоднородной). Система является гомогенной, если все ее составные части находятся в одном агрегатном состоянии, т.е. между ними отсутствует поверхность раздела. Примером такой системы является плазма крови. В гетерогенной системе можно выделить поверхность раздела между различными составляющими этой системы, таким системам характерна неоднородность, они содержат несколько фаз. Фаза –
27
однородная часть системы с одинаковыми химическими и термодинамическими свойствами, отделенная от других частей видимой поверхностью раздела, при переходе через которую физические и химические свойства резко изменяются. Различные биологические объекты, такие как, человек или клетки живых организмов являются примерами гетерогенных систем.
Реакции, протекающие в гомогенной системе, развиваются во всем ее объеме, и называются гомогенными. Реакции, происходящие на границе раздела фаз, называются гетерогенными.
Совокупность всех физических и химических свойств системы называется состоянием системы. Состояние системы характеризуется
параметрами, которые подразделяются на экстенсивные и интенсивные.
Экстенсивные параметры – параметры, значения которых пропорциональны числу частиц в системе (масса, объем, количество вещества). Интенсивные параметры – параметры, значения которых не зависят от количества частиц в системе (температура, давление).
Параметры, описывающие состояние системы, называются функциями. Одним из свойств любой функции состояния является независимость ее изменения от способа, или, как говорят, от пути реализации процесса. Функции состояния могут быть использованы для создания уравнения, описывающего термодинамический процесс (закон Бойля–Мариотта, уравнение Клайперона–Менделеева). Эти уравнения позволяют описать конкретный термодинамический процесс, что и является конечной целью термодинамики.
§2. Первый закон термодинамики. Энтальпия
В 1840г. немецкий врач Юлиус Роберт Майер (1814 – 1878) работал на острове Ява. В те годы обычной медицинской процедурой было кровопускание. Майер обратил внимание на то, что венозная кровь матросов, которых он лечил, светлее, чем была в северных широтах, и близка по цвету артериальной. Майер знал: изменение окраски крови связано с поглощением кислорода (насыщенная кислородом артериальная кровь светлее лишенной кислорода венозной). Ученый смог дать правильное объяснение обнаруженному им явлению. В жарком климате для поддержания постоянной температуры тела организм должен вырабатывать меньше теплоты, поэтому на окисление пищи расходуется меньше кислорода и кровь почти не темнеет. В 1842г. Майер сформулировал важнейший для термодинамики вывод о том, что теплота и работа могут превращаться друг в друга. Кроме того, он впервые установил количественное соотношение между теплотой и работой,
вычислив так называемый механический эквивалент теплоты.
28
Формулирование первого закона термодинамики завершил в 1850 г. немецкий физик Рудольф Юлиус Эмануэль Клаузиус (1822–1888). Из принципа эквивалентности теплоты и работы, заключил он, следует, что система обладает особым свойством, изменение которого равно алгебраической сумме теплоты и работы. Позднее это свойство получило название внутренней энергии (U).
Одна из основных функций состояния системы – полная энергия системы Е, которая представляет собой сумму трех составляющих: кинетической энергии Екин. движущейся системы, потенциальной энергии Епот., обусловленной воздействием на систему внешних силовых полей, и внутренней энергии системы U:
E=Eкин +Eпот +U
При термодинамическом описании предполагают, что система находится в состоянии относительного покоя (Екин.=0) и воздействие внешних полей пренебрежимо мало (Епот.=0). Тогда полная энергия системы определяется запасом ее внутренней энергии (Е=U). Для термодинамического анализа характеристической величиной является изменение внутренней энергии при переходе системы из одного состояния в другое. Внутренняя энергия, как и любое термодинамическое свойство системы, является функцией состояния, т.е. изменение ее не будет зависеть от того, через какие промежуточные стадии идет процесс, а будет определяться только исходным и конечным состоянием системы. Это положение вытекает из закона сохранения энергии, согласно которому
энергия не исчезает и не возникает вновь, а лишь переходит из одной формы в другую в строго эквивалентных соотношениях. В
соответствии с этим законом, выражающим первое начало термодинамики, общий запас внутренней энергии остается постоянным, если отсутствует тепловой обмен с окружающей средой, т.е. в изолированных системах, в ходе процессов возможно лишь перераспределение внутренней энергии между отдельными составляющими системы.
Первый закон термодинамики является частным случаем закона сохранения энергии применительно к макроскопическим системам. Согласно первому закону термодинамики
Сообщенная системе теплота расходуется на приращение внутренней энергии и на совершение работы против внешних сил:
Q= U+A
Уравнение представляет собой математическое выражение первого начала термодинамики.
29
Выражение работы против внешних сил, в частности, против внешнего давления, в изобарно-изотермических условиях, в которых функционируют живые организмы, может быть записано:
A=p V, тогда Q (U2 U1) p(V2 V1)
Qp (U2 U1) p(V2 V1) (U2 pV2) (U1 pV1) H2 H1 H
Через U1,U2 обозначен запас внутренней энергии в исходном и конечном состояниях, V1,V2 – значения объема в исходном и конечном состояниях системы. Вводя функцию состояния системы H=U+p V,
называемую энтальпией (теплосодержанием) системы получаем:
Q=H2 -H1 H
Название энтальпия (от греч. «энтальпо» – «нагреваю») ввел нидерландский физик Хейке Камерлинг – Оннес.
Количество теплоты, которое выделяется или поглощается при проведении химических реакций в изобарно-изотермических условиях, характеризуется изменением энтальпии системы и называется энтальпией реакции ∆Нр.
Химические реакции, сопровождающиеся поглощением или выделением теплоты, подразделяются на экзотермические и
эндотермические.
Экзотермические процессы сопровождаются выделением энергии из системы в окружающую среду. В результате таких процессов энтальпия системы уменьшается (∆Н<0).
Эндотермические процессы сопровождаются поглощением энергии системой из окружающей среды, следовательно, энтальпия системы повышается (∆Н>0).
Энтальпия системы является экстенсивным параметром и зависит от количества вещества, температуры и давления, поэтому изменение энтальпии в результате химической реакции определяют при стандартных условиях.
Стандартные условия: давление – 760 мм рт. ст.=101325 Па Температура – 298 К ≈25°С
Значения ∆Н зависят от природы веществ, и от условий их существования, и от характера рассматриваемого процесса. Поэтому их принято унифицировать, относя к так называемому стандартному состоянию. Под последним подразумевают стандартные значения давления и температуры, для кристаллических и жидких веществ их устойчивое состояние при р=1 атм., а для газов их состояние под атмосферным давлением и при условии, что они обладают свойствами, присущими им при очень низких давлениях, т.е. являются идеальными газами. Для веществ в растворе принимают их концентрацию С(Х) = 1 моль/л, причем предполагается, что раствор ведет себя, как и при весьма
30
