5Сетевые модели (n-схемы)

1. . Пусть процесс функционирования некоторой реальной системы S (процессор ЭВМ, мультиплексный канал, станок в технологической цепочке и т. п.), являющийся по своей природе процессом обслужива­ния, представлен в виде двухфазной одноканальной Q- схемы:

Пусть имеется некоторая система S, например, производственно-технологическая, процесс функционирования которой представлен в виде Q-схемы:

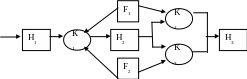
По технологическому циклу для выполнения заказа необходимо выпол­нить две фазы обслуживания: сначала обслуживание в канале К1, затем либо в К2, либо в К3. Операторы F1 и F2 обслуживают (поддерживают в работоспособном состоянии) каналы, причем F1 об­служивает К, и К2, a F2 — K1 и К3. Тогда в этой системе могут быть следующие состояния:

а — заказ пришел и ждет в на­копителе Н1;

б — заказ обработан К1, и ждет в накопителе Н2;

в— заказ выполнен и находит­ся в накопителе Н3;

г — канал К1, не занят;

д — канал К2 не занят;

е — канал К3 не занят;

ж — оператор F1 не занят;

з — оператор F2 не занят;

и — канал К1, выполняет заказ под управлением F1;

к — канал К1, выполняет заказ под управлением F2;

л — канал К2 выполняет заказ под управлением F1

м — канал К3 выполняет заказ под управлением F2

и могут происходить следующие события-пере­ходы:

1— поступление заказа;

2— F1 начинает выполнение заказа на К;

3— F1 закончил выполнение заказа на К;

4— F2 начинает выполнение заказа на К1;

5— F2 закончил выполнение заказа на К1;

6— F1 начинает выполнение заказа на К2;

7— F1 закончил выполнение заказа на К2;

8— F2 начинает выполнение заказа на К3;

9— F2 закончил выполнение заказа на К3;

10— заказ отправляется на доставку.

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.

5.2 Рассмотрим процесс функционирования ЭВМ с конвейерной обработкой. При построении высокопроизводительных асинхронных ЭВМ широко применяют метод конвейерной обработки чисел. Этот метод обработки подобен функционированию сборочного конвейера и особенно удобен для работы с век торами в массивами. Конвейер состоит из набора операций, которые могут выполняться одновременно в разных блоках ЭВМ. Когда операция в k-м блоке завершается, ее результат передается в (k+ 1)-й блок, a k-й блок принимает результат операции из (k - 1)-го блока. Если каждая операция запускается по завершении предыдущей, то имеем дело с асинхронным способом управления конвейером. Для управления k-м блоком такого конвейера необходима информация о выполнении следующих условий:

входной регистр заполнен;

входной регистр пуст;

выходной регистр заполнен;

выходной регистр пуст;

блок k занят;

блок k свободен;

пересылка осуществляется.

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.

5.3 Рассмотрим принципы программирования N-схем в языке MODAL, который предназначен для моделирования и реализации вычислительных алгорит­мов на базе N-схем (сетей Петри). Он содержит семь операторов:

START — описание начальной маркировки;

STOP — описание конечной маркировки;

T(MOD) — описание структуры сети Петри;

T YPE — оператор промежуточного вывода на печать;

СOMMENT

COMPLEKXITY - вспомогательные операторы;

END — конец

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.

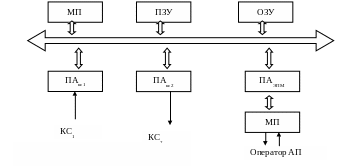
5.4 Построим в виде N-схемы модель микропроцессорного абонентского пункта (АП) информационно-вычислитель­ной сети. Структура этого АП показана на рисунке, где обозначено: МП — микро­процессор; ОЗУ — оперативное запомина­ющее устройство; ПА — периферийный адаптер; ЭПМ — электрифицированная пи­шущая машинка; КС1 и КС2 — входной и выходной каналы связи. Задание N_s-схемы в виде временной се­ти включает в себя задание структуры <B, D, I, O>, вектора разметок М₀ и вектора задержек Z.

Структуру N_s -схемы зададим графически, так как именно графическое представ­ление обладает наибольшей наглядностью и простотой соотношения со структурой объекта, т. е. в данном примере со структурой АП. На рисунке для наглядности пунктиром выделены элементы N_s-схемы, относящиеся к конкретным элементам структуры АП.

Вектор разметок имеет вид М₀ = (010100001110000001 N_b0), а вектор задержек

Z = (z_BX, 0, z_KC1, 0, 0, z_лм1,0, z_ЛМ, 0, 0, 0, z_ВХ2, z_ПМ2, О, z_КС1, 0,0).

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.

5.5 Поступление метки во входную позицию перехода d_m инициирует процедуру проверки готовности перехода к срабатыванию. Проверяемые при этом условия включают в себя анализ разметки решающей позиции M{b_k}, где , а также проверку разметки выход­ных позиций M{О(d_m)} и сопряженных позиций M{I(d_m)}. В том случае, когда , на данной фазе производится также вычисление решающей процедуры перехода z (d_m).

При достижении требуемых условий переход вступает в ак­тивную фазу, содержание которой определяется элементами описания перехода i(d_m) и p(d_m), причем элемент t(d_m) может быть задан либо непосредственно, либо в виде функции. В по­следнем случае необходимо предварительно вычислить эту фун­кцию, а затем моделировать требуемое время t (d_m).

Процедура перехода p(d_m) выполняется в два этапа: сна­чала вычисляются предикаты П_j, а затем реализуется требуемое подмножество операций над описателями меток {l_jp }. Далее переход d_m вступает в фазу завершения, содержанием которой является смена разметки входных и выходных позиций перехо­да М {I(d_m)} и M(O(d_m)}. Разметка позиции b_i, меняется на нулевую: M(b_i):=0. При разметка решающей позиции становится неопределенной: M(b_k):=e⁰. Затем выполняется пе­ремещение меток в ряд выходных позиций O(d_m) в соответствии с типом данного перехода. Эта операция завершает работу перехода по обработке поступившей метки.

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.

5.6 Проведем анализ соответствия между элементами N_E - схем и объектами языка моделирования GPSS. В результате сравнительного анализа можно сформулировать следующее.

1. Метка N_E-схемы может быть представлена динамическим объектом GPSS, т.е. транзактом.

2. Описатели меток аналогичны парамет­рам транзактов GPSS.

3. Позиция N_E-схемы идентична объекту, принадлежащему к аппаратной категории GPSS типа накопителя единичной емкости.

4. Решающие позиции 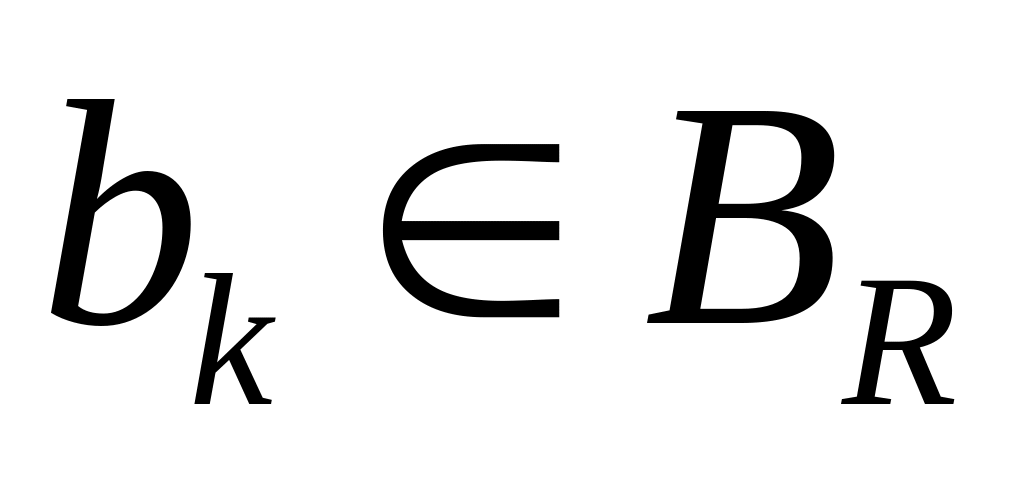N_E схемы в зависимости от принадлежности к множеству В_p реализуются двумя способами:

а) если , то b_k эквивалентна набору объектов типа булевых переменных вычислительной категории GPSS;

б) если , то b_k может быть представлена накопителем единичной емкости аппаратной категории GPSS.

5. Временные параметры переходов I (d_m) реализуются объектом ADVANCE операционной категории GPSS.

6. Операции вычисления предикатов П_j, 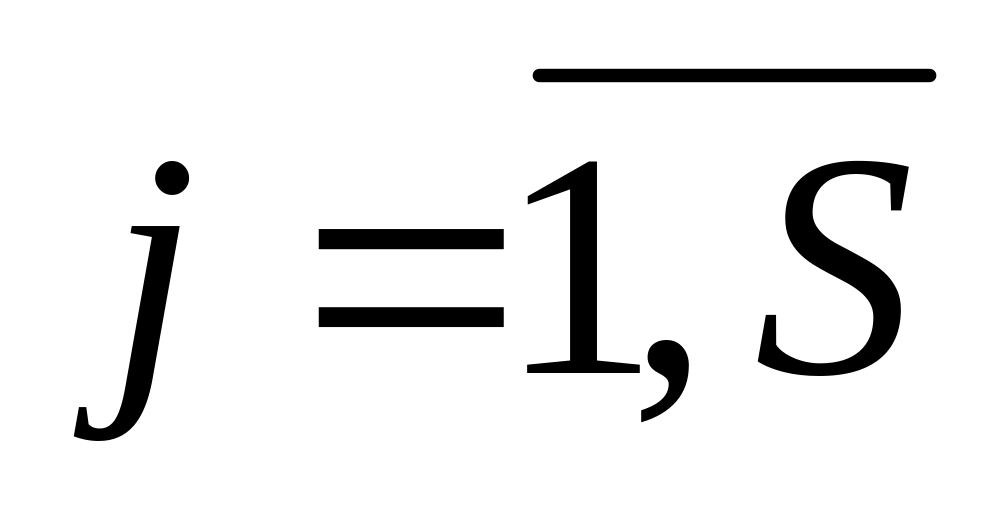, для p(d_m) соответствует применение блока TESTE, изменяющего маршруты транзактов, в сочетании с булевыми переменными вычислительной категории GPSS.

7. Операции {l_jp} для p(d_m) выполняются с помощью блоков ASSIGN динамической категории GPSS в сочетании с арифметическими переменными.

8. Хранение значений описателей меток можно имитировать путем записи значений параметров транзактов в ячейки хранимых значений (X, ХН) с помощью блока SAVEVALVE запоминающей категории GPSS.

9. Процессы синхронизации движения меток через переход d_m и удаления меток из решающей позиции , могут быть обеспечены с помощью огических переключате­лей LOG IC S и LOGIC R аппаратной катего­рии GPSS.

10. Макропозиция генератора аналогична блоку GENERATE динамической катего­рии GPSS.

11. Макропозиция поглощения функционально идентичена блоку ERMINATE динамической категории GPSS.

12. Макропозиция очереди может интерпретироваться в GPSS записью транзакта в цепь пользователя.

Формализовать процесс при помощи N-схемы, считая, что состояниям системы соответствуют позиции N-схемы, событиям — переходы. Нанести маркировку, соот­ветствующую такому состоянию системы, при котором каналы свободны, операто­ры не заняты, в системе нет заказов.