2.3 Расчет систем массового обслуживания с отказами методом Монте-Карло

Рассмотрим одну из самых простых систем массового обслуживания. Система эта состоит из n-линий (или каналов, или пунктов обслуживания), каждый из которых может обслуживать потребителей. В систему поступают заявки, причем моменты их поступления случайные. Каждая заявка поступает на линию № 1. Если в момент поступления k-й заявки (назовем его Т_к) эта линия свободна, то она приступает к обслуживанию заявки, что продолжается t₃ мин. (t₃ – время занятости линии). Если в момент Т_к линия № 1 занята, то заявка мгновенно передается на линию № 2. и т.д… Если все n-линии в момент Т_к заняты, то система выдает отказ. Требуется определить, сколько (в среднем) заявок обслужит система за время Т и сколько отказов она даст. Ясно, что задачи такого типа встречаются при исследовании организации работы любых предприятий, а не только предприятий бытового обслуживания. Здесь метод Монте-Карло является единственным методом расчета.

Схема расчета. Каждой линии поставим в соответствие ячейку внутреннего накопителя ЭВМ, в которую будем записывать момент, когда эта линия освобождается. Обозначим момент освобождения i-й линии через t_i. За начальный момент расчета выберем момент поступления первой заявки T₁=0. Можно считать, что в этот момент все t_i равны T₁: все линии свободны. Время окончания расчета Т_кон =Т₁+Т.

Первая заявка поступает на линию №1. Значит, в течение t₃ линия эта будет занята. Поэтому заменяем t₁ на новое значение (t₁)_нов = Т₁+t₃ , добавить единицу к счетчику выполненных заявок и перейти к рассмотрению второй заявки. Предположим, что к заявок уже рассмотрены. Тогда разыграем момент поступления (к+1)-й заявки. Для этого выбираем очередное значение γ и по формуле τ = 1/а lnγ вычисляем очередное значение τ = τ_к. А затем вычисляем момент поступления Т_к+1 = Т_к+τ_к. Свободна ли в этот момент первая линия? Для установления этого надо проверить условие t₁ <=T_k+1. Если это условие выполнено, то значит, к моменту Т_к+1 линия уже освободилась и может обслуживать эту заявку. Мы должны заменить t₁ на T_k+1+t₃, добавить единицу к счетчику выполненных заявок и перейти к следующей заявке. Если условие t₁ <=T_k+1не выполнено, то значит, что первая линия в момент T_k+1 занята. Тогда проверяем, свободна ли вторая линия t₂ <=T_k+1. Если условие t₂ <=T_k+1 выполнено, то заменяем t₂ на T_k+1+t₃, добавляем единицу к счетчику выполненных заявок и переходим к следующей заявке. Если предыдущее условие не выполнено, то переходим к проверке условия t₃ <=T_k+1. Может оказаться, что при всех i от 1 до n t_i > T_k+1, т.е. все линии в момент Т_к+1 заняты. Тогда надо добавить единицу в счетчик отказов и потом перейти к рассмотрению следующей заявки. Каждый раз, вычислив Т_к+1, надо проверять еще условие окончания опыта Т_k+1 > Т_кон .Когда это условие окажется выполненным, опыт заканчивается. В счетчике выполненных заявок и в счетчике отказов будут стоять числа μ_вып и μ_отк. Такой опыт повторяется N раз (с использованием различных γ). И результаты всех опытов усредняются: ; , где μ_{вып (j)} и μ_{отк (j)} – значения μ_вып и μ_отк, полученные в j-ом опыте.

Представим блок-схему программы, реализующий расчет СМО методом Монте-Карло на рис. 7. [17]

J= 1

Т₁ = 0; t₁ = t₂ = … = t_n = 0; k = 1

Конец опыта

i = 1

J: = J +1

Подсчет результатов, выдача, конец задачи

t_i <= T_k

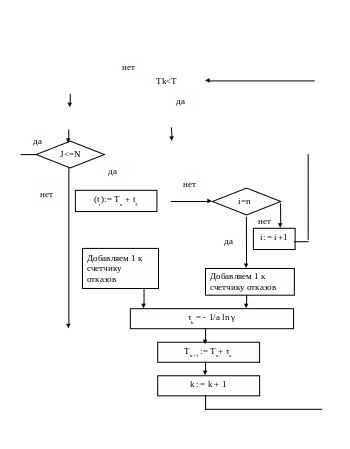
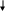
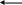
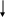
Рисунок 7 - Блок-схема программы, осуществляющей расчет СМО методом Монте-Карло

Пример. В трехканальную систему массового обслуживания с отказами поступает пуассоновский поток заявок. Время между поступлениями двух последовательных заявок распределено по показательному закону f(τ) = 5e^-5τ . Длительность обслуживания каждой заявки равна 0,5мин. Найти методом Монте-Карло математическое ожидание а числа обслуженных заявок за время Т=4мин.

Решение: Пусть Т₁=0 – момент поступления первой заявки. Заявка поступит в первый канал и будет им обслужена. Момент окончания обслуживания первой заявки Т₁+0,5=0+0,5=0,5. В счетчик обслуженных заявок записываем единицу.

Моменты поступления последующих заявок найдем по формуле:

Т_i=T_i-1+τ_i.

где τ_i - длительность времени между двумя последовательными заявками с номерами i-1 и i.

Возможные значения τ_i разыгрываем по формуле

Учитывая, что, по условию, λ=5, получим τ_i=0,2 (ln r_i).

Случайные числа r_i берем из таблицы приложения 1, начиная с первой строки сверху. Для нахождения времени между поступлениями первой и второй заявок возьмем случайное число r₁=0,10.

Тогда вычислим: τ₂=0,2*(ln0,10)=0,2*2,30=0,460.

Первая заявка поступила в момент Т₁ = 0. Следовательно, вторая заявка поступит в момент Т₂ = Т₁+0,460=0,460. В этот момент первый канал ещё занят обслуживанием первой заявки, поэтому вторая заявка поступит во второй канал и будет им обслужена. Момент окончания обслуживания второй заявки Т₂+0,5=0,460+0,5=0,960. В счетчик обслуженных заявок добавляем единицу.

По очередному случайному числу r₂=0,09 разыграем время τ₃ между поступлениями второй и третьей заявок:

τ₃ = 0,2*(-ln 0,09) = 0,2*2,41=0,482.

Вторая заявка поступила в момент Т₂=0,460. Поэтому третья заявка поступит в момент Т₃=Т₂+0,482=0,460+0,482=0,942. В этот момент первый канал уже свободен, и третья заявка поступит в первый канал. Момент окончания обслуживания третьей заявки Т₃+0,5=1,442. В счетчик обслуженных заявок добавляем единицу.

Дальнейшие расчеты производят и результаты записывают в таблице, причем если в момент поступления заявки все каналы заняты (момент поступления заявки меньше каждого из моментов окончания обслуживания), то в счетчик отказов добавляют единицу. Заметим, что обслуживание 20-й заявки закончится в момент 4,148>4, поэтому эта заявка получает отказ.

Таблица 1

№ заявки, i	Случай-ное число, ri	-ln ri	Время между двумя послед. заявками τi=0.2(ln ri)	Момент поступ-ления заявки Тi=Тi-1+τi	Момент Тi+0,5 окончания обслуживания заявки каналом			Счетчик
					1	2	3	обс. заявок	отка-зов
				0	0,500			1
	0,10	2,30	0,460	0,460		0,960		1
	0,09	2,41	0,482	0,942	1,442			1
	0,73	0,32	0,064	1,006		1,506		1
	0,25	1,39	0,278	1,284			1,784	1
	0,33	1,11	0,222	1,506	2,006			1
	0,76	0,27	0,054	1,560		2,060		1
	0,52	0,65	0,130	1,690					1
	0,01	4,60	0,920	2,610	3,110			1
	0,35	1,05	0,210	2,820		3,320		1
	0,86	0,15	0,030	2,850			3,350	1
	0,34	1,08	0,216	3,066					1
	0,67	0,40	0,080	3,146	3,646			1
	0,35	1,05	0,210	3,356		3,856		1
	0,48	0,73	0,146	3,502			4,002		1
	0,76	0,27	0,054	3,556					1
	0,80	0,22	0,044	3,600					1
	0,95	0,05	0,010	3,610					1
	0,90	0,010	0,020	3,630					1
	0,91	0,09	0,018	3,648	4,148				1
	0,17	1,77	0,354	4,002 (стоп)					1
							Ито-го	х1=12	8

Испытания прекращают (в таблице записывают «стоп»), если момент поступления заявки Т>4. Из таблицы находим, что за 4 мин. всего поступило 20 заявок; обслужено х₁=12 заявок.

Выполнив аналогично ещё пять испытаний, получим: х₂=15, х₃=14, х₄=12, х₅=13, х₆=15.

В качестве оценки искомого математического ожидания а числа обслуженных заявок примем выборочную среднюю

=(2*12+13+14+2*15)/6=13,5

Пример. В одноканальную систему массового обслуживания с отказами поступает пуассоновский поток заявок. Время между моментами поступления двух последовательных заявок распределено по закону f(τ)=0,8е^-0,8τ; время обслуживания заявок случайное и распределено по закону f₁(t)=1,5е^-1,5t. Найти методом Монте-Карло за время Т=30мин: среднее число обслуженных заявок; среднее время обслуживания одной заявки; вероятность обслуживания; вероятность отказа. Произвести 6 испытаний.

Решение. Время между моментами поступления двух последовательных заявок распределено по закону f(τ)=0,8е^-0,8τ, поэтому значения τ_i разыграем по формуле: τ_i = -(1/0,8)ln r_i = 1,25(-ln r_i).

Случайные числа r_i берем из таблицы равномерно распределенных случайных чисел, начиная с первой строки снизу. Время обслуживания заявок распределено по закону f₁(t)=1,5е^-1,5t, поэтому значения t_i разыгрываем по формуле:

t_i = -(1/1,5)ln R_i = 0,67 (-ln R_i).

Случайные числа R_i, берем из той же таблицы, начиная с первой строки сверху. Пусть Т₁=0 – момент поступления первой заявки. По случайному числу R₁=0,10 разыгрываем длительность времени обслуживания первой заявки (в мин): t₁ = 0,67 (-ln 0,10) = 0,67*2,30 = 1,54.

Момент окончания обслуживания первой заявки Т₁=1,54=0+1,54=1,54. В счетчик обслуженных заявок записываем единицу.

По случайному числу r₂=0,69 разыграем время (в мин) между моментами поступления первой и второй заявок: τ_i = 1,25 (-ln 0,69) = 1,25*0,37=0,46.

Первая заявка поступила в момент Т₁=0. Следовательно вторая заявка поступит в момент Т₂=Т₁+0,46=0+0,46=0,46.

В этот момент канал занят обслуживанием первой заявки (0,46<1,54), поэтому вторая заявка получит отказ. В счетчик отказов записываем единицу.

По очередному случайному числу r₃=0,07 разыгрываем время между моментами поступления второй и третьей заявок:

τ₃ = 1,25 (-ln 0,07) = 1,25*2,66 = 3,32.

Вторая заявка поступила в момент Т₂=0,46. Следовательно, третья поступит в момент Т₃=Т₂+3,32=0,46+3,32=3,78. В этот момент канал уже свободен (3,78>1,54), поэтому он обслужит третью заявку. В счетчик обслуженных заявок добавляем единицу.

Дальнейший расчет ясен из таблиц 2 и 3. Испытание заканчивается, когда момент поступления заявки Т_i>30. Например, в первом испытании, как видно из табл. 2, 23-я заявка поступила в момент Т₂₃=31,35>30, поэтому эту заявку исключаем («Стоп») и первое испытание заканчиваем [2].

Таблица 2

Номер заявки i	Случайное число ri	-ln ri	Время между двумя последовательными заявками τi = 1.25 (-ln ri)	Момент поступления заявки Тi=Ti-1+τi
1.				0
2.	0,69	0,37	0,46	0,46
	0,07	2,66	3,32	3,78
	0,49	0,71	0,89	4,67
	0,41	0,89	1,11	5,78
	0,38	0,97	1,21	6,99
	0,87	0,14	0,18	7,17
	0,63	0,46	0,58	7,75
	0,79	0,24	0,30	8,05
	0,19	1,66	2,08	10,13
	0,76	0,27	0,34	10,47
	0,35	1,05	1,31	11,78
	0,58	0,54	0,68	12,46
	0,40	0,92	1,15	13,61
	0,44	0,82	1,02	14,63
	0,01	4,60	5,75	20,38
	0,10	2,30	2,88	23,26
	0,51	0,67	0,84	24,10
	0,82	0,20	0,25	24,35
	0,16	1,83	2,29	26,64
	0,15	1,90	2,38	29,02
	0,48	0,73	0,91	29,93
	0,32	1,14	1,42	31,35 (стоп)

Таблица 3

Номер заявки i	Случайное число Ri	-ln Ri	Длительность обслуживания заявки ti=0,67 (-ln Ri)	Момент			Счетчик
				Поступления заявки	Начала обслуживания	Окончания обслуживания	Обслуженных заявок	отказов
1.	0,10	2,30	1,54	0	0	1,54	1
2.				0,46				1
3.	0,09	2,41	1,61	3,78	3,78	5,39	1
4.				4,67				1
5.	0,73	0,32	0,21	5,78	5,78	5,99	1
6.	0,25	1,39	0,93	6,99	6,99	7,92	1
7.				7,17				1
8.				7,75				1
9.	0,33	1,11	0,74	8,05	8,05	8,79	1
10	0,76	0,27	0,18	10,13	10,13	10,31	1
11.	0,52	0,65	0,44	10,47	10,47	10,91	1
12.	0,01	4,60	3,08	11,78	11,78	14,86	1
13				12,46				1
14.				13,61				1
15.				14,63				1
16.	0,35	1,05	0,70	20,38	20,38	21,08	1
17.	0,86	0,15	0,10	23,26	23,26	23,26	1
18.	0,34	1,08	0,72	24,10	24,10	24,82	1
19.				24,35				1
20.	0,67	0,40	0,27	26,64	26,64	26,91	1
21.	0,35	1,05	0,70	29,02	29,02	29,72	1
22.	0,48	0,73	0,49	29,93	30,42			1
Σ			11,71				13	9

Таблица 4

Номер испытания i	Поступило заявок N i пост	Обслужено заявок N i обсл.	Длительность обслуживания t i обсл	Среднее время обслуживания tср i обсл= t i обсл /Ni обсл.	Вероятность обслуживания Р i обсл= N i обсл / Ni пост	Вероятность отказа Рiотк.= 1-Рi обсл.
1.	22	13	11,71	0,90	0,591	0,409
2.	25	17	8,80	0,52	0,680	0,320
3.	24	16	13,46	0,84	0,667	0,333
4.	22	15	12,19	0,81	0,682	0,318
5.	20	13	11,99	0,92	0,650	0,350
6.	27	19	9,57	0,50	0,704	0,296
Σ	140	93		4,49	3,974

Используя таблицу 4, найдем искомые величины:

а) среднее число обслуженных за 30мин заявок N_обсл. =93/6=15,5;

б) среднее время обслуживания одной заявки t_обсл. =4,49/6=0,748;

в) вероятность обслуживания Р_обсл.=3,974/6=0,662;

г) вероятность отказа Р_отк. =1-Р_обсл.=1-0,662=0,338.

Таким образом, примерно 66% заявок будут обслужены, а 34% получат отказ.