1.2.3. Третя аксіома механіки Ньютона.

Ця аксіома має ще одну назву: закон рівності дії та протидії. З цією аксіомою ми зустрічались в статиці. Для двох матеріальних точок вона формулюється наступним чином: при взаємодії двох матеріальних точок сила, що діє на перше тіло з боку другого, рівна за величиною та протилежна за напрямком силі, що діє на друге тіло з боку першого.

Нехай маємо систему, що складається з двох тіл з масами m₁ та m₂.

В цій системі, як видно на рисунку 1.2.3., можуть діяти лише дві сили: (сила, що діє на тіло 2 з боку тіла 1) та (сила, що діє на тіло 1 зі сторони тіла 2).

Ці сили називаються силами взаємодії.

Третій закон Ньютона стверджує, що при взаємодії двох тіл .

	Необхідно відмітити, що сили, котрі входять до третього закону Ньютона, прикладені до різних тіл і не складають зрівноваженої системи сил. Сила називається реакцією у відношенні до , а сила - реакцією у відношенні до . Третій закон динаміки проявляється при дослідженні руху в будь-якій системі відліку.
Рисунок 1.2.3. Взаємодія двох тіл.

1.2.4. Четверта аксіома механіки Ньютона.

Ця аксіома має ще одну назву: принцип незалежності дії сил. Якщо на матеріальну точку діє водночас декілька сил, тоді вектор прискорення цієї точки дорівнює геометрічній сумі прискорень, що мала б точка при дії кожної сили окремо.

;

.

1.3. Диференціальне рівняння руху точки.

В кінематиці вивчались 3 способи завдання руху точки:

• векторний;

• координатний;

• - натуральний.

Для кожного з цих способів в динаміці можна визначити рух векторним рівнянням, рівняннями в проекціях на прямокутні осі координат, а також природними рівняннями руху.

1.3.1. Диференціальне рівняння руху точки в векторній формі.

Якщо рух точки масою т задано в векторній формі як наведено на рисунку 1.3.1., то її положення в просторі визначається радіус-вектором :

	. Прискорення точки М в цьому випадку виражається через радіус-вектор : . Рівняння приймає вигляд:
Рисунок 1.3.1. Рух точки заданий в векторній формі.

.

Рівняння називається рівнянням руху матеріальної точки у векторній формі.

1.3.2. Диференціальні рівняння руху точки в прямокутних координатах.

	З кінематики відомо, що рух точки у прямокутних координатах задається рівняннями: . Для рішення задач динаміки точки треба мати рівняння, що зв'язують координати x, y, z цієї точки та діючу на неї силу (або сили).
Рисунок 1.3.2. Рух точки заданий в прямокутних координатах.

Розглянемо матеріальну точку, яка рухається під дією сил по відношенню до інерціальної системи відліку Oxyz, як наведено на рисунку 1.3.2.

Проектуючи обидві частини рівняння на вісі x, y, z, маємо:

де a_x , a_y , a_z , F_x , F_y , F_z – проекції прискорення точки М та силы на на координатні осі.

Проекції прискорення можна виразити через другі похідні по часу від координат точки, що рухається:

; ; .

Отримаємо:

; ; .

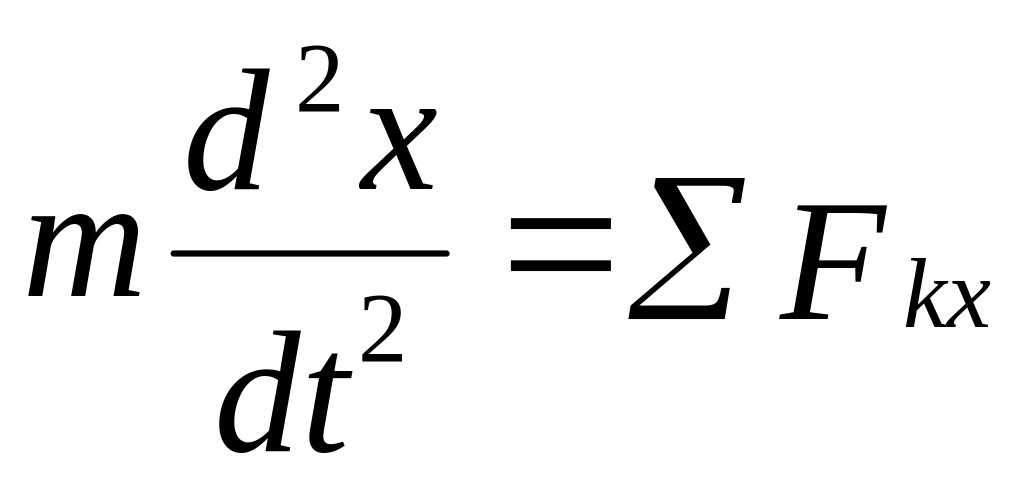Або, позначая другі похідні за часом двома точками:

; ; .

Ці рівняння називаються диференціальними рівняннями руху матеріальної точки в прямокутних координатах.

Система трьох диференціальних рівнянь (2.5) другого порядку еквівалентна системі шести диференціальних рівнянь першого порядку:

; ; .

; ; .

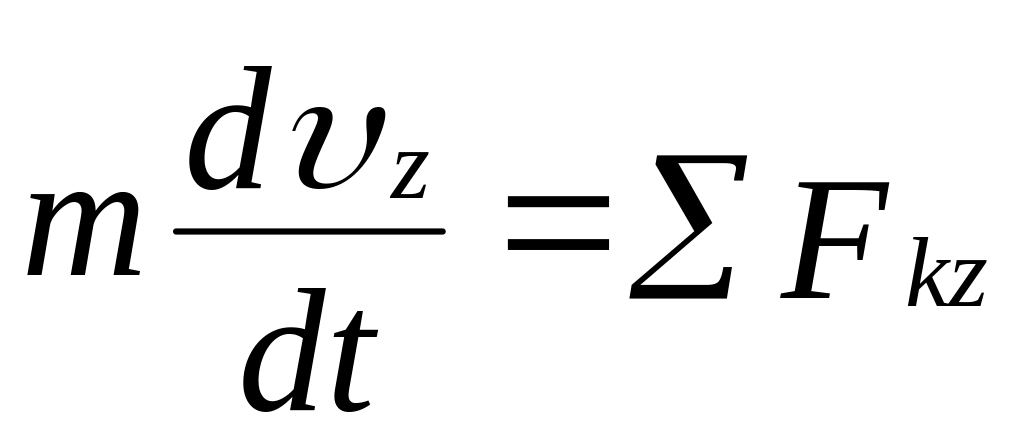Якщо точка М рухається в площині ОХY , то Z = 0, , знаходимо:

; .

У випадку руху точки вздовж прямої лінії, спрямувавши по ній координатну вісь ОХ, отримаємо одне диференціальне рівняння прямолінійного руху точки

.