6 . Неперервна функція

Озн.1 Ф-я f(x), x [a,b] наз-ся неперервною в x₀ [a,b], якщо границя ф-ї f(x) в т.x₀ iснує і дорівнює значенню ф-ї в цій точці: lim f(x)=lim f(x₀)

О зн.2 Ф-я f(x) наз. неперервною в т.x₀, якщо вона визначена в околі точки і границя приросту функції в цій точці дорівнює 0, якщо

^y

y _ _ _ _ _ _ _ _ _ ­­­_

lim f(x) = 0 y₀_ ^y _ _ _ _ _ _ _

0 x₀ x x ^x

О зн.3 Ф-я f(x) наз. неперервною зліва в т. x₀, якщо lim f(x)=f (x₀) і

^-0

неперервною справа, якщо lim f(x)= f(x₀)

⁺⁰

О зн.4. Ф-я f(x) наз. неперервною на будь-якому інтервалі (a,b),якщо вона неперервна в кожній точці цього інтервалу.

Властивості функції неперервної в точці на відрізку

1. Сума скінченого числа ф-ій , неперервних на будь-якому проміжку (а,в) у точці х₀, є ф-я неперервна в цій точці.

2. Добуток скінченого числа ф-й, неперервних в точці х₀, є неперервна ф-я в точці ч₀ .

3. Частика двох функцій, неперервних в точці х₀ є ф-я неперервна в т.х₀, якщо значення ф-ії в знаменнику не дорівнює 0 в х₀.

4. Якщо f(x) неперервна то lim f(x) = f (lim x)

5. Якщо ф-я f(x) неперервна на [a,b] і на його кінцях приймає значення різних знаків, то на [a,b] знайдеться хоча б одна точка, в якій ф-я дорівнює 0.

6.Якщо ф-я неперервна на [a,b] то на ньому існує найбільше i найменше значення функції.

Класифікація точок розриву функції

Якщо т. x₀ належить обл.. визначення ф-ії, або її межі і не є точкою неперервності то кажуть , що x₀ - точка розриву ф-ії. Це можливо в слідуючи випадках:

1) в т. x₀ ф-ія не визначена

2)не існує границя ф-ії при x x₀

3)границя існує, але вона не дорівнює значенню ф-ії в т.x_0.

О зн.5 Точка розриву функції наз. Точкою розриву 1 роду, якщо ф-я має скінченні границі зліва та справа.

lim f(x) = f (x₀-0); lim f(x)= f (x₀+0)

^{0 0}

О зн.6 Якщо границя зліва і справа скінченні числа, маємо стрибок.

Озн.7 Точка x₀ розриву першого роду, в якій f (x-0)=f (x+0) f(x) наз. точкою усуненого розриву.

О зн.8 Якщо ф-я на відрізку [a,b] має лише скінченне число точок розриву 1 роду, то її наз. кусочно-неперервною.

Озн.9 Якщо хоча б одна границя справа або зліва дорівнює нескінченності маємо розрив 2 роду.

розрив 2 роду

7. Чудові границі

1.Перша чудова границя

lim або lim

Доведення

Розгл. дугу кола радіуса R=1, з центральним кутом х ( 0<x< /2 ) ОА =1 sin x = MK ; tg x = AT(1)

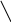
_М ^Т S OAM < S_cekOAM<S OAT.

_х 1/2OA^. MK<1/2 OA^. AM<1/2OA^. AT. Використаємо

О К А рів-я (1) 1/2 sin x< 1/2 x<1/2tg x => sinx<x<tgx/sinx (2)

1> >cos

0<1- <1-cos x , т.я.sin x/2 <1 то sin² x/2< sin x/2 враховуючи (2) х, яке належить (0, ) маємо 1-соs x - 2sin² x/2< 2 sin x/2<2^. x/2

т.ч. 0<1- <x, візьмемо >0, = min{ , } => x ,виконаємо перевірку х< => 0<1- => => 1= -до тогож

- парна => ліва границя в т.х=0=1 ⁰

• l im .

Приклад.

2.Друга чудова границя.

^u = ^{1/ u} = e

Доведення.

Раніше доведимо, що lim (1+ ) ⁿ = e, доведимо, що lim (1+ ) ^x = e.

Нехай х>1;n=[x]=> x = n + де n N, [0;1)Т.я. n x<n+1 то ⁿ < ^x < ^{n +1} при х (n )

lim (1+ ) ⁿ⁺¹ = lim ⁿ lim = e 1=e

lim ⁿ = = = e => lim ^x = e.

Розгл. х<-1, нахай х = -у, => ^x = ^-y = ^y =

^y

= ^y-1 =e ^. 1 =e при х

Приклад.

lim ^{x / 2} = e

^x

^x =lim ^{( x-2) / 4* (4/ (x-2)) * x} = e ^{lim 4x / x-2} =e⁴