3.4. Ньютон әдісі (жанамалар әдісі).
Мейлі
кесіндісінде
теңдеуінің түбірі айырылған, және де
үздіксіз және
кесіндісінде таңбалары тұрақты болсын.
Бұл
әдістің геометриялық мағынасы
төмендегідей:
жуықтауы
нүктесінде
қисық сызығына жүргізілген жанаманың
осімен қиылысу нүктесінің абсциссасына
тең (а-сурет). Сондықтан оны жанамалар
әдісі деп те атайды.
І-жағдай. Мейлі , , , (сурет-а) немесе , , , (сурет-б).
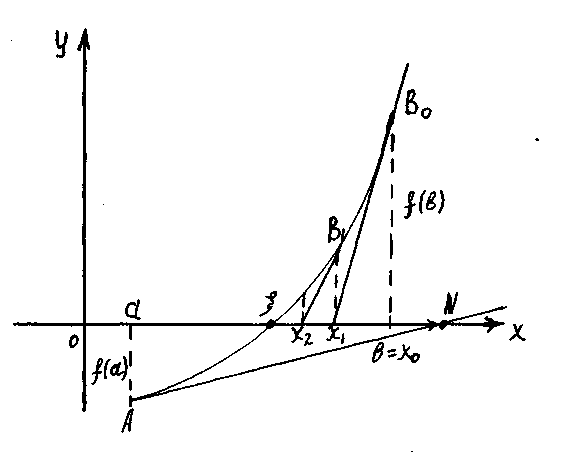
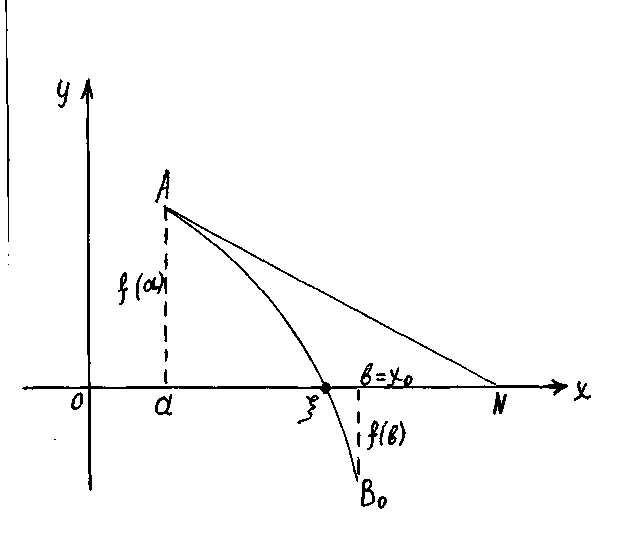
қисығына нүктесінде жанама жүргізіп оның осімен қиылысу нүктесінің абсциссасын табамыз. Осы жанаманың теңдеуі
Айталық
,
деп
(1)
табамыз.
Енді теңдеудің түбірі
кесіндісінде жатады. Тағы да Ньютон
әдісін қолданып,
нүктесінде қисыққа жанама жүргізіп,
-ні
табамыз
.
Ары қарай жалғастырсақ
(2)
Осылайша
түбірдің
жуық мәндерінің тізбегін аламыз, оның
әрбір келесі мүшесі оның алдындағы
мүшеден түбірдің дәл мәніне
жақынырақ. Бірақ та
түбірдің дәл мәнінен
үлкен болады, яғни
-
түбірдің артығымен алынған жуық мәні.
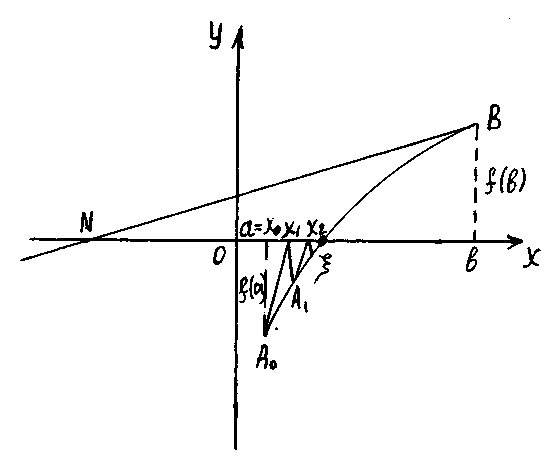
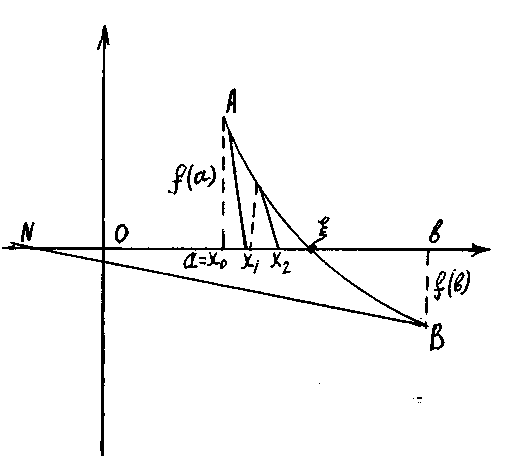
а) б)
Егер В
нүктесінен
қисығына жанама жүргізсек, оның
осімен
қиылысу нүктесі
кесіндісінде жатпайды. Сондықтан
жанаманы
нүктесінен жүргіземіз, оның теңдеуі
Айталық , деп
(3)
табамыз.
Енді теңдеудің түбірі
кесіндісінде жатады. Тағы да Ньютон
әдісін қолданып,
нүктесінде жанама жүргізсек, онда
.
Ары қарай жалғастырсақ
(4)
Алынған жуық мәндердің тізбегінің әрбір келесі мүшесі түбірдің шын мәніне жақындай түседі, ал -түбірдің дәл мәнінің кемімен алынған жуық мәні болады.
І
және ІІ жағдайды салыстырсақ, олардың
бір-бірінен айырмашылығы алғашқы
жуықтауды алуда, яғни І-жағдайда
,
ІІ-жағдайда
.
Түбірдің алғашқы жуықтауын мына ережені пайдаланып алу керек: алғашқы нүкте үшін кесіндісінің, функция мен оның екінші туындысының таңбалары бірдей болатын ұшын аламыз.
Қателікті бағалау үшін мына формуланы пайдалануға болады
(5)
мұнда
.
Бұл
формула хорда әдісі үшін де жарайды.
кесіндісі өте кішкене болған жағдайда,
онда
шарты орындалса, мұнда
,
,
онда
-ші
итерациядағы жуықтаудың дәлдігі
былайша бағаланады:
егер
болса, онда
Егер
кесіндісінде
өте аз өзгеретін болса, онда есептеулерді
жеңілдету үшін мына формуланы қолдануға
болады
,
(6)
яғни
туындының мәнін алғашқы нүктеде бір
рет есептеу жеткілікті.Бұның геометриялық
мағынасы
нүктесінде жанама,
нүктесінде жүргізілген жанамаға
параллель түзумен ауыстырылады.
Мысал
1.
теңдеуінің [-2,75; -2,5] кесіндісінде
орналасқан түбірін жанамалар әдісімен
дәлдікпен
анықта.
Шешуі.
f
(-2,75) · f"
(х)>0
болатындығы бұрын анықталған (мысал 1,
хордалар әдісі). Сондықтан жанамалар
әдісін қолдану үшін
деп
аламыз. Есептеулерді (6)-шы формула
бойынша жүргіземіз. Табамыз
Барлық есептеулерді келесі кестеге орналастырамыз:
n
|
|
|
|
|
|
- |
0 1 2 3 4 5 |
-2,75 -2,571 -2,545 -2,537 -2,534 -2,533 |
-20,797 -16,994 -16,484 -16,329 -16,271 |
7,5625 6,6100 6,4770 6,4364 6,4212 |
22,6875 19,8300 19,431 19,309 19,2636 |
-1,111 -0,164 -0,053 0,020 0,007 |
0,179 0,026 0,008 0,003 0,001 |
Бұл
кестеден
<0,001,
сондықтан
