3.2. Түбірлерді айырудың аналитикалық әдістері Ол үшін математикалық талдау курсынан белгілі, функциялардың кейбір қасиеттерін пайдаланамыз.

Теорема 1. Егер үздіксіз функциясы кесіндісінің ұштарында әр түрлі таңбалы мәндер қабылдаса, онда осы кесіндісінің ішінде теңдеуінің ең болмағанда бір түбірі болады.

Теорема 2. Егер функциясы кесіндісінде монотонды және үздіксіз болса және кесіндінің ұштарында әр түрлі таңбалы мәндер қабылдаса, онда осы кесіндінің ішінде теңдеуінің тек бір ғана түбірі болады.

Теорема 3. Егер функциясы кесіндісінде үздіксіз және кесіндінің ұштарында әр түрлі таңбалы мәндер қабылдаса, ал туындысының осы кесіндінің ішінде таңбасы өзгермейтін болса, онда кесіндісінің ішінде теңдеуінің түбірі болады және ол біреу болады.

Аналитикалық әдіспен түбірді былай айыруға болады:

1. Бірінші туындыны табамыз.

2. - ті туындының критикалық мәніне не шекаралық мәнге тең деп болжап,

функциясының таңбасының кестесін құрамыз.

3. Ұштарында функция қарама-қарсы таңбалы мәндер қабылдайтын интервалдарды анықтаймыз. Бұл интервалдардың ішінде тек бір ғана түбірден болады.

Мысал. теңдеуінің түбірін аналитикалық әдіспен айырыңыз.

Шешуі. ден белгілейміз. f(x) – функциясының анықталу облысы (- ). Функцияның бірінші туындысын табымыз

Бұл туындыны нульге теңеп, түбірін табамыз

; ; ;

х: а) критикалық мәндерге (туындының түбірлері) немесе оған жақын;

б) шекаралық мәндерге (белгісіздің мүмкін мәндер облысынан шығатын) тең деп болжап f(x) функциясының таңбаларының кестесін құрамыз:

х	-	2	3	+
sign x	+	-	-	+

Функциясының таңбасы екі рет өзгергендіктен, теңдеудің екі түбірі болады.

Түбір айыру операциясын аяқтау үшін, түбірлер жататын аралықтарды, ұзындығы 1-ден үлкен болмайтындай етіп кішірейту керек. Осы аралықтарға сәйкес жаңа кесте құрамыз:

х	-1	0	1	2	3	4	5
sign f(x)	+	-	-	-	-	-	+

Теңдеудің түбірлері (-1;0) және (4;5) аралықтарында жатады.

3.3. Хордалар әдісі

теңдеуі берілсін, мұнда - интервалында бірінші және екінші ретті туындылары бар, үздіксіз функция болсын. Түбірі айырылған және кесіндісінде жатады делік, яғни .

Хордалар әдісінде, жеткілікті кішкене аралығында қисығы оны керетін хордамен алмастырылады. Түбірдің жуық мәні үшін хорданың осімен қиылысу нүктесі қабылданады.

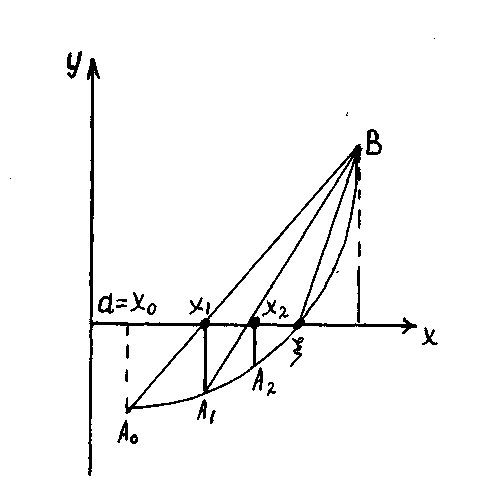І. Функцияның І-ші және ІІ-ші ретті туындыларының таңбалары бірдей болған жағдайын қарастырайық, яғни . Мейлі , , , болсын. Функцияның графигі , нүктелері арқылы өтсін. функциясының графигінің осімен қиылысу нүктесі теңдеуінің түбірі болады. Бұл нүкте бізге белгісіз, сондықтан оның орнына хордасының осімен қиылысу нүктесін -ді аламыз. Бұл түбірдің жуық мәні болады.

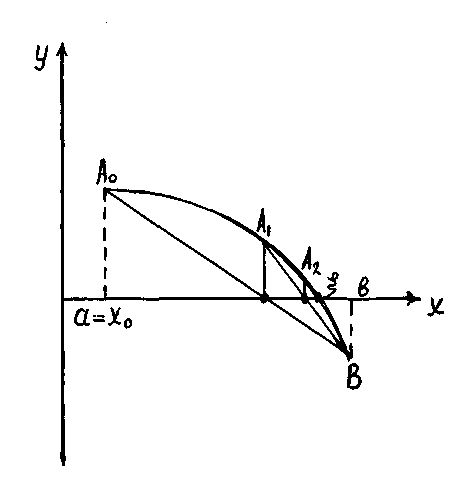1-ші сурет

және нүктесі арқылы өтетін хорданың теңдеуі .

мәнін табамыз, онда . Сонда,

(1)

Бұл хордалар әдісінің формуласы деп аталады.

Енді теңдеудің түбірі кесіндісінде жатады. Егер түбірдің мәні бізді қанағаттандырмаса, онда кесіндісіне хордалар әдісін қолданып, түбірдің мәнін дәлірек анықтаймыз. , нүктелерін қосып, хордасының осімен қиылысу нүктесі -ні табамыз.

Бұл процесті ары қарай жалғастырсақ

,..., (2)

Бұл процесті түбірдің жуық мәні берілген дәлдікпен табылғанша жалғастырамыз.

Бұл формуламен , , , болған жағдайда да есептеуге болады. (1б-сурет).

ІІ. Енді І-ші және ІІ-ші ретті туындының таңбалары әр түрлі болған жағдайды қарастырайық. .

Мейлі , , , болсын. және нүктелерінен өтетін хорданың теңдеуін жазайық:

деп болжап, хорданың осімен қиылысу нүктесі -ді табайық (3)

Теңдеудің түбірі аралығында жатады.

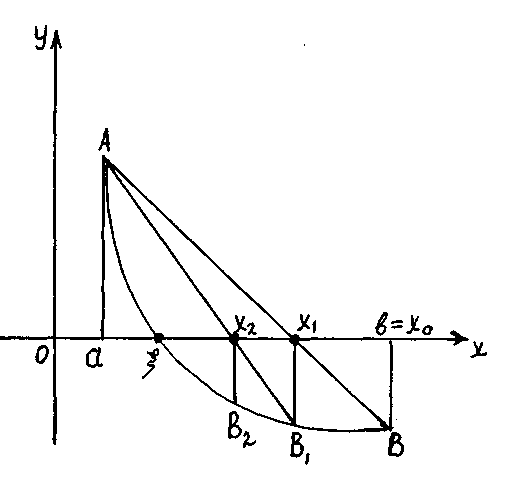
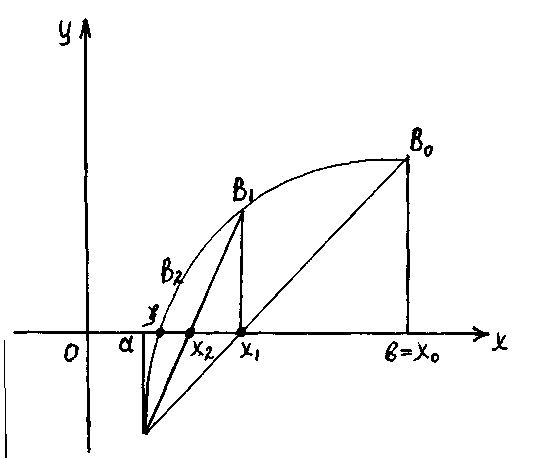a) б)

кесіндісіне хорда әдісін қолданып, -ні табамыз.

(3¹)

Жалпы

(4)

Бұл формуламен , , , болған жағдайда түбірді табуға болады (2б-сурет).

Сонымен, егер болса, жуық түбір 1-ші және 2-ші формуламен, ал егер болса, 3-ші және 4-ші формуламен есептеледі. Бұл формулаларды мына ереже бойынша таңдаймыз:

Кесіндінің қозғалмайтын ұшы үшін, функцияның және оның екінші туындысының таңбалары бірдей болатын ұшты аламыз.

Егер болса онда в ұшы қозғалмайтын, ал түбірге а ұшынан жақындаймыз. (1-ші және 2-ші формула). Егер болса, онда а ұшы қозғалмайтын, ал түбірге в ұшынан жақындаймыз (3-ші және 4-ші формула).

Жуықтаудың қателігін бағалау үшін мына формуланы пайдаланамыз (5)

түбірдің дәл мәні, -ші және -ші жуықтаудың мәні. Бұл формула мына жағдайда орынды

. (6)

Мұнда ,

Мысал 1. теңдеуінің кіші түбірін хорда әдісімен ε=0.001 дәлдікпен анықта. Теңдеудің түбірлері айырылған және кіші түбірі [-3; -2] кесіндісінде жатады.

Шешуі. (6)-шы шарттың орындалуын тексереміз:

< 2m.

[-3, -2] кесіндісінің ортасын аламыз, яғни х=-2,5 нүктесін, сөйтіп [-3; -2,5] кесіндісін таңдаймыз. (6)-шы шарттың орындалуын тексереміз:

М<2m.

Енді [-3; -2,5] кесіндісінің ортасы– х=-2,75 нүктесін аламыз; f (2,75) <0, f (-2,5)>0, f (-3)<0 болғандықтан [-2,75; 2,5] кесіндісін таңдаймыз. Табамыз

яғни бұл жағдайда M<2m шарты орындалады.

Сонымен, [-2,75; -2,5] кесіндісінде жататын түбірдің қателігін бағалау үшін (5)-ші формуланы қолдануға болады:

<

яғни түбірге жүйелі жақындау процессін шарты орындалғанша жүргіземіз.

Екінші туындының таңбасын анықтап, қай формуламен есептеулер жүргізу керектігін анықтаймыз. Табамыз на отрезке [-2,75; -2,5] кесіндісінде теңсіздіктері орындалады. Сондықтан кесіндінің қозғалмайтын ұшы үшін x=2,75 аламыз. Сонда есептеулерді (3) және (4) формулалармен жүргіземіз:

мұнда а=-2,75 және f(a)=-1,111. Егер соңғы өрнекті мына түрге келтірсек

онда бірден екі жүйелі жуықтаудың арасындағы айырмашылықты және есептеулердің аяқталуын тексере аламыз, яғни теңсіздігінің орындалуын тексереміз.

Барлық есептеулерді келесі кестеде орындаған ыңғайлы:

n							-
0 1 2 3	-2,5 -2,525 -2,531 -2,5319	-15,625 -16,098 -16,213	6,250 6,3756 6,4060	18,75 19,1268 19,2180	0,125 0,0288 0,0050	0,25 0,225 0,219	-0,025 -0,006 -0,0009

Бұл кестеден, <0,001, сондықтан мыңдық бірлікке дейін дөңгелектеп екенін аламыз.