2.5. Түбірдің салыстырмалы қателігі

Мейлі , онда

. (2.9)

Яғни m-ші дәрежелі түбірдің салыстырмалы қателігі түбір астындағы санның салыстырмалы қателігінен m есе кіші.

Мысал. Егер квадраттың ауданы S=12.34 абсолюттік қателігі болса, оның қабырғасын қандай салыстырмалы қателікпен және қанша дұрыс цифрымен табуға болады.

Шешуі: ;

.

Осы жерден ( -ге жақын бүтін сан).

2.6. Қателіктің жалпы формуласы Мейлі дифференциалданатын функция

және и - функцияның аргументтерінің абсолюттік қателіктері берілсін. Онда функцияның абсолюттік қателігі

немесе

. (2.10)

U-ға бөліп салыстырмалы қателікті аламыз:

. (2.11)

Мысал. Шардың көлемінің абсолюттік және салыстырмалы қателігін тап, егер см, болса.

Шешуі: см².

см³; %.

2.7. Есептеулер жүргізудің жалпы ережесі

Жалпы есептеулер жүргізуде келесі ережелерді пайдалану ұсынылады:

1. Жуық сандарды қосу, алу, көбейту және бөлу нәтижесінде сонша мәнді цифрды қалдыру керек, дұрыс цифрлар саны ең кіші жуықтап берілгендердің қанша мәнді цифры болса.

2. Дәрежеге шығарғанда негізінде қанша мәнді цифр болса сонша мәнді цифрды сақтау керек.

3. Егер кейбір берілгендердің кіші ондық разрядтары артық (қосуда және алуда) немесе басқаларға қарағанда мәнді цифрлары көп болса (көбейтуде, бөлуде, дәрежеге шығаруда), онда оларды алдын-ала бір цифрын артық сақтап дөңгелектеу керек.

4. Егер берілгендерді еркін дәлдікпен алуға болса, онда нәтижені n дұрыс цифрымен алу үшін, бастапқы берілгендерді нәтижені n+1 цифрмен қамтамасыз ететін цифрлар санымен алу керек. Одан кейін нәтиже бір цифрға дөңгелектенеді.

2.8. Қателіктер теориясының кері есебі

Практикада кері есеп те өте маңызды: функцияның абсолюттік қателігі берілген шамадан аспауы үшін оның аргументтерінің абсолюттік қателіктері қандай болуы керек.

Бұл есеп математикалық түрде анықталмаған, себебі функцияның берілген толық абсолюттік қателігін қамтамасыз ету үшін оның аргументтерінің абсолюттік қателіктерінің шектерін әр түрлі етіп қоюға болады.

Кері есептің қарапайым шешімі тең әсер принципімен алынады. Бұл принцип бойынша, қателіктердің қосындысындағы барлық қосылғыштардың жалпы абсолюттік қателіктің пайда болуына әсері бірдей деп болжанады.

Мейлі берілсін делік. Онда

болады. Айталық барлық қосылғыштар бір-бірімен тең болсын, онда

.

Осы жерден

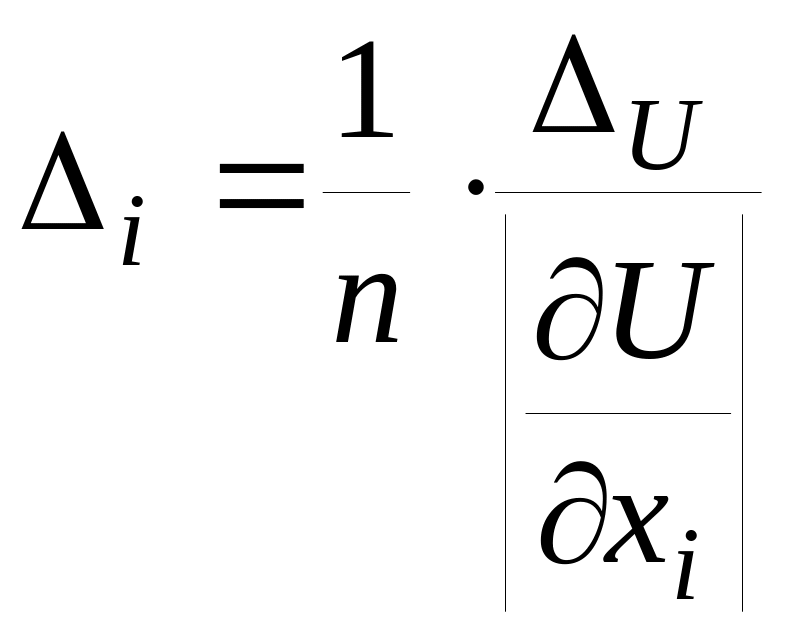(i=1…n). (2.12)

Мысал. Цилиндрдің табанының радиусы м, биіктігі м болсын. Цилиндрдің көлемін 0.1 м³ дәлдікпен есептеу үшін, R және H-ты қандай абсолюттік қателіктермен алу керек.

Шешуі:

,

; (қосылғыштар саны).