9.6. Параболалық түрдегі теңдеулер үшін шектеулі айырымдық әдіс.
Жылу өткізгіштік теңдеу үшін аралас есепті қарастырайық.
Біртекті
біліктің (стерженнің) жылу өткізгіштік
теңдеуін қарастырайық.
мұндағы
-температура,
-уақыт,
-меншікті
жылу сыйымдылығы,
-тығыздық,
-жылу
өткізгіштік коэффициент,
деп ұйғарайық,
ауыстыру көмегімен барлық уақытта
осылай етуге болады
(1)
теңдеуін аламыз.
Уақыттың
бастапқы мезетінде
температураның таралуы
(2)
және
стерженнің шеткі нүктелерінде
температураның уақытқа тәуелді өзгеру
заңдары берілсін
(3)
-жеткілікті
тегіс функциялар және
Уақыттың
кез келген мезетінде
температураның білік бойымен таралуын
табу керек. (1) – (3) аралас есептің шешімі.
облысында
ізделінеді
-жабық
тіктөртбұрыш,
-жартылай
ашық тіктөртбұрыш.
кесіндісін
өзара тең
-ны
өзара тең
бөліктерге бөлеміз.
-
натурал сандар
және
бойынша қадамдар.
,
торлар құрамыз.
теңдеудегі туындыларды
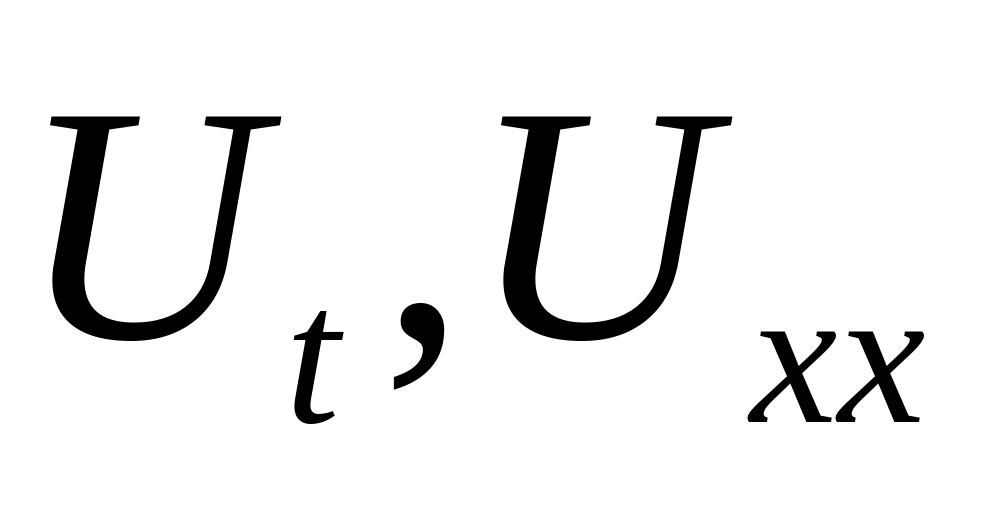-ті
айырымдық қатынастармен
алмастырамыз
(4)
деп
белгілейік,
-тұрақты.
Сонда (4)-ші теңдеуден аламыз
(6)
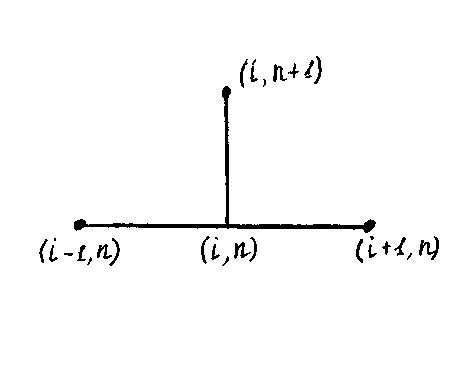
шамасын таңдағанда,
(1) дифференциалдық теңдеуді (4)
шектеулі-айырымдық теңдеумен алмастырғанда
қателік ең кіші болатындай етіп аламыз.
Белгілеу енгіземіз
,
мұндағы
-
дифференциалдық операторына сәйкес
келетін шектеулі айырымдық оператор.
-айырмасы
аппроксимация қателігі деп аталады.
Осы
қателікті (1) теңдеудің шешімі
функциясы үшін
тораптарында есептейміз.
және
,
,
екенін
ескеріп,
-ды
нүктесінің аймағында реті
-дейінгі
мүшемен шектеп, Тейлор формуласы бойынша
жіктейміз.
Бақылау сұрақтары
1. Аралас шекаралық есеп деген не
1. Орынды қойылған есеп деген не?
2. Торлар, торлық функция деген не?
3. Айырымдық схемалардың жинақтылығы.
4. Айырымдық схемалардың аппроксимациясы
5. Айырымдық схемалардың орнықтылығы.
6. Ішек тербелісінің айырымдық схемасын жазыңыз.
7. Ішек тербелісінің айырымдық схемасының орнықтылық шарты.
8. Жылу өткізгіштік теңдеуінің айырымдық схемасын жазыңыз.