Бақылау сұрақтары

33. Қандай жағдайда сандық интегралдау әдістері қолданылады?

34. Сандық интегралдау әдістері қандай идеяға негізделген?

35. Квадратуралық формула дегеніміз не?

36. Ньютон-Котес квадратуралық формуласын жазыңыз

37. Тіктөртбұрыштар формуласын жазыңыз.

38. Тіктөртбұрыштар формуласының қалдық мүшесі.

39. Трапеция формуласын жазыңыз.

40. Трапеция формуласының геометриялық интерпретациясын беріңіз.

41. Трапеция формуласының қалдық мүшесін жазыңыз.

42. Трапеция формуласы немесе орта тіктөртбұрыштар формуласының қайсысы дәлірек?

43. Симпсон формуласын жазыңыз.

44. Симпсон формуласының қалдық мүшесін жазыңыз.

45. Симпсон формуласының геометриялық интерпретациясын беріңіз.

8. Жәй дифференциалдық теңдеулер

8.1. Жалпы мәліметтер

Есептің қойылымы. Механиканың, физиканың, химияның тағы басқа ғылымдардың және техниканың көптеген есепетерінің математикалық модельдері дифференциалдық теңдеуге алып келеді.

Тәуелсіз айнымалы шамалардың санына байланысты дифференциалдық теңідеулер екі түрге бөлінеді: жәй дифференциалдық теңдеулер – бір тәуелсіз айнымалы шамасы бар; дербес туындылы теңдеулер – бірнеше тәуелсіз айнымалы шамалары бар.

Кейбір жағдайларда диффференциалдық теңдеуден оның жоғарғы ретті туындысын айқын түрде өрнектеп жазуға болады.

Бұндай теңдеулерді жоғарғы ретті туындысына байланысты шешілген теңдеулер деп атаймыз.

Жәй дифференциалдық теңдеудің шешімінің сызбасын интегралдық қисық деп атаймыз.

Дифференциалдық теңдеудің дербес шешімін алу үшін берілетін қосымша шарттар түріне байланысты екі түрлі есеп пайда болады: Коши есебі және шекаралық есеп. Қосымша шарттар ізделініп отырған функцияның және оның туындыларының кейбір нүктедегі мәнімен беріледі.

Егер бұл шарттар бір нүктеде берілсе, ондай есеп Коши есебі деп, қосымша шарттар алғашқы шарттар деп, ал бұл шарттар берілген нүкте -алғашқы нүкте деп аталады.

Егер қосымша шарттар бірнеше нүктеде берілетін болса, яғни тәуелсіз айнымалының әртүрлі мәндерінде, ондай есеп шекаралық есеп деп, ал қосымша шарттар шекаралық шарттар деп аталады.

Әдетте шекаралық шарттар екі нүктеде және диффееренциалдық теңдеудің шешімдерінің облысының шекарасында беріледі.

Коши есебінің қойылымының мысалдары:

Шекаралық есептер.

8.2. І-ші ретті дифференциалдық теңдеудің сандық шешімі

Эйлер әдісі

Жәй дифференциалдық теңдеудің Коши есебінің сандық шешімін табудың қарапайым әдісі Эйлер әдісі болады.

(1) теңдеуінің кесіндісінде бастапқы (1¹) шартты ( егер болса) қанағаттандыратын сандық шешімін табу керек. кесіндісін нүктелерімен бірдей бөлікке бөлеміз. - қадам, функциясы 1-ші теңдеудің жуық шешімі болсын және Белгілейміз .

нүктелерінде 1-ші теңдеудегі туындыны ақырлы айрыммен айырбастаймыз.

(2), (2¹)

Егер болса, онда

немесе

Бұл теңдікте белгілі демек

Егер болса, онда немесе ,

Мұнда белгілі, анықталатын Ары қарай ,

(3)

Осылайша нүктелерінде жуық шешімнің мәні анықталады.

Э

йлер әдісінің блок схемасы.

Эйлер әдісінің геометриялық интерпретациясы. Мына суретте торлық функцияның нүктелеріндегі мәнін есептеу бейнеленген. Интегралдық қисықтар 0,1,2 (1) теңдеудің дәл шешімін бейнелейді. 0-ші қисық Коши есебінің (1,1¹) дәл шешімін береді, себебі ол нүктесі арқылы өтеді. В,С нүктелері есепті Эйлер әдісімен шешкенде пайда болған. Бұл қисықтардың «0» қисығынан ауытқуы Эйлер әдісінің қателігін береді. Әрбір қадам орындалған сайын біз жаңа интегралдық қисыққа түсеміз. АВ – «0»-ші қисыққа Ф нүктесінде жүргізілген жанама . ВС – 1-ші қисыққа жүргізілген жанама. Сонымен Эйлер әдісі әрбір қадам сайын жаңа интегралдық қисыққа алып келеді. Әрбір қадамдағы есептеудің қателігі (локальдық қателік).

нүктесінен қашықтықта жатқан нүктесіндегі шешімді тапқанда, әрбір нүктедегі қателіктер қосылады яғни . Егер болса, онда қателіктердің қосындысы

нүктелерін түзу сызықтармен қосып интегралдық қисықты жуықтап бейнелейтін Эйлер сынығын аламыз. Эйлер сынығы интегралдық қисыққа нүктелерінде жүргізілген жанамалардан тұратын сынық сызық.

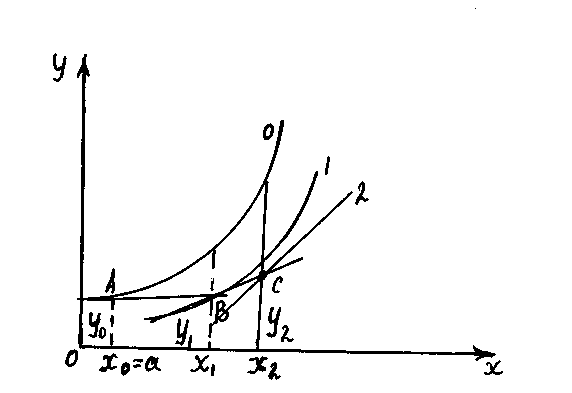
- қадамы кішірейген сайын шешімнің дәлдігі жоғарылайды ( -қатенің шамасы).

Эйлер әдісінің модификациясы. Жетілдірілген Эйлер әдісі. Бұл әдістің негізі мынада: алдымен ізделініп отырған функцияның нүктедегі көмекші мәнін табамыз

(4)

Енді осы нүктедегі (1)-теңдеудің оң жағының мәнін табамыз . Сонда

. (5)

Эйлер-Коши немесе Эйлердің қайта санау әдісін функцияны Тейлор қатарына жіктеу арқылы алуға болады. Бұл жіктеу былай жазылады

. (6)

Бұл схемада h² бар мүше сақталу керек. Ол үшін екінші ретті туындыны ақырлы айырымдармен аппроксимацмялаймыз

(7)

Бұл байланысты (6)-ға қойып, мынаны аламыз

. (8)

Туындыларды мына өрнекпен алмастырамыз

. (9)

(8)-ші схема айқындалмаған схема, себебі оның екі жағына да ізделініп отырған шамасы кіреді. Сондықтан -ді есептеу үшін итерациялық әдістердің біреуін пайдаланамыз. Егер алғашқы жуықтау жақсы болса, онда екі итерацияда шешімді алуға болады. -алғашқы жуықтау деп, бірінші жуықтауды аламыз

(10)

-дің жаңа мәнін (6,7) формулада -дің орнына қойып, мынаны аламыз

(11)

Бұл тәсіл әдістің қателігін бағалауға мүмкіндік береді. Әдістің әрбір қадамдағы (локальдық) қателігінің реті h³, ал суммарлық қателігінің реті h².

Мысал 1. Эйлердің қайта санау әдісін пайдаланып, кесіндісінде бастапқы шартты қанағаттандыратын, дифференциалдық теңдеуінің интегралының жуық мәнінің кестесін құр; қадам h=0,1. Барлық есептеулерді төрт ондық таңбамен орындау керек.

Шешуі. Эйлердің қайта санау әдісі бойынша, әрбір мән мұнда у(х) – ізделінді функция, ал k=0, 1, 2, …, былай анықталады:

Алғашқы жуықтау үшін

где

алынады; табылған мән мына формуламен қайта саналады

(i=1, 2, …).

Соңғы тізбектелген екі жуықтаудың айырымы берілген дәлдікті қанағаттандырғанда, қайта санауды тоқтатамыз.

Барлық есептеулерді келесі кестені құрып жүргізген ыңғайлы:

негізгі кесте (кесте. І), мұнда есептің жауабы жазылады;

кесте (кесте. ІІ), мұнда тізбектелген жуықтау процессі орындалады;

көмекші кесте (кесте. ІІІ), мұнда функциясының мәні есептеледі.

Кесте І.

k
0 1 2 3 4 5 6 7 8 9 10	1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4	2,2 2,4306 2,6761 2,9357 3,2084 3,4929 3,7876 4,0908 4,4006 4,7152 5,0328	2,2292 2,3821 2,5281 2,6648 2,7895 2,8998 2,9936 3,0696 3,1268 3,1654	0,2229 0,2382 0,2528 0,2665 0,2790 0,2900 0,2994 0,3070 0,3127 0,3165

Кесте ІІ.

k+1
1	1,5	2,2	0 1 2	2,4229 2,4305 2,4306	2,2292	2,3805 2,3820 2,3821	4,6097 4,6112 4,6113	0,2305 0,2306 0,2306
2	1,6	2,4306	0 1 2	2,6688 2,6760 2,6761	2,3821	2,5268 2,5280 2,5281	4,9089 4,9101 4,9102	0,2454 0,2455 0,2455
3	1,7	2,6761	0 1	2,9289 2,9357	2,5281	2,6641 2,6648	5,1922 5,1929	0,2596 0,2596
4	1,8	2,9357	0 1	3,2022 3,2084	2,6648	2,7892 2,7895	5,4540 5,4543	0,2727 0,2727
5	1,9	3,2084	0 1	3,4874 3,4929	2,7895	2,8998 2,8998	5,6893 5,6893	0,2845 0,2845
6	2,0	3,4929	0 1	3,7829 3,7876	2,8998	2,9939 2,9936	5,8937 5,8934	0,2947 0,2947
7	2,1	3,7876	0 1	4,0870 4,0908	2,9936	3,0700 3,0696	6,0636 6,0632	0,3032 0,3032
8	2,2	4,0908	0 1	4,3978 4,4006	3,0696	3,1278 3,1268	6,1969 6,1964	0,3098 0,3098
9	2,3	4,4006	0 1	4,7133 4,7152	3,1268	3,1658 3,1654	6,2926 6,2922	0,3146 0,3146
10	2,4	4,7152	0 1	5,0517 5,0328	3,1654	3,1866 3,1863	6,3520 6,3517	0,3176 0,3176

Кесте ІІІ.

k	x	y
0	1,4	2,2	0,9778	0,8292	2,2292
1	1,5 1,5 1,5	2,4229 2,4305 2,4306	1,0768 1,0802 1,0803	0,8805 0,8820 0,8821	2,3805 2,3820 2,3821
2	1,6 1,6 1,6	2,6688 2,6760 2,6761	1,1861 1,1893 1,1894	0,9268 0,9280 0,9281	2,5268 2,5280 2,5281
3	1,7 1,7	2,9289 2,9357	1,3017 1,3048	0,9641 0,9648	2,6641 2,6648
4	1,8 1,8	3,2022 3,2084	1,4232 1,4260	0,9892 0,9895	2,7822 2,7695
5	1,9 1,9	3,4874 3,4929	1,5500 1,5524	0,9998 0,9998	2,8998 2,8998
6	2,0 2,0	3,7829 3,7876	1,6813 1,6834	0,9939 0,9936	2,9939 2,9936
7	2,1 2,1	4,0870 4,0908	1,8164 1,8181	0,9700 0,9696	3,0700 3,0696
8	2,2 2,2	4,3978 4,4006	1,9546 1,9558	0,9273 0,9268	3,1273 3,1268
9	2,3 2,3	4,7133 4,7152	2,0948 2,0956	0,8658 0,8654	3,1658 3,1654
10	2,4 2,4	5,0317 5,0328	2,2363 2,2368	0,7866 0,7863	3,1866 3,1863

І кестеде алынған -тің мәндері, есептің жауабы болады.