4.5.2. Жүйені итерациялық процеске дайындау

Итерация әдісін қолдану үшін, берілген жүйенің жолдарының орынын ауыстып, жүйенің матрицасының диагоналінің бойында модулі бойынша ең үлкен коэффициент тұруы қажет. Егер бұл жағдайда (3.5.5) шарты орындалмаса, онда келесі әдістің көмегімен әдістің жинақты болуын қамтамасыз етуге болады.

Айталық жүйесі берілсін. Оны мына түрге келтіреміз

,

мұнда

; (3.5.6)

.

Бұл жерде - кейбір матрица. Бізге шарты орындалатын матрицасын таңдау қажет.Келесі теореманы дәлелдейік.

Теорема 2. Егер матрицасының диагональдық элементтері келесі шартты қанағаттандырса

, (3.5.7)

онда итерация әдісі алғашқы жуықтауға тәуелсіз жинақты болады.

Дәлелдеуі:

Зерттеуді мына мөлшер үшін жүргіземіз

.

Келесі белгілеулерді енгіземіз:

- матрицасының -ші жолы;

- матрицасының -ші жолы;

- матрицасының -ші жолы;

- матрицасының (бірлік вектор) -ші жолы.

Бұл белгілеулерді пайдаланып (4.3.6) теңдігін мынадай түрде жазуға болады

, (3.5.8)

мұнда где - және векторларының скалярлық көбейтіндісі.

(3.5.8)-ден мынаны аламыз

. (3.5.9)

, мұнда - скалярлық шамасын алайық. Егер үшін шамасын алсақ, онда (4.3.9) теңсіздігінің оң жағындағы бірінші қосылғышы нульге айналып, мынаны аламыз

.

Себебі , онда (3.5.7) шартын ескерсек

. (3.5.10)

(3.5.10) теңсіздігін ескеріп екенін аламыз, демек, 1-ші теоремаға сәйкес итерациялық процессі жинақты болады. Теорема дәлелденді.

матрицасы мынадай түрге келеді , мұнда - диагональдық матрица.

Ескерту. Егер матрицасы үшін матрицасын алсақ, онда (3.5.6) теңдігінде және векторы болады.

4.5.3. Зейдель әдісі

Зейдель әдісін жәй итерация әдісінің модификациясы түрінде көрсетуге болады.

Мейлі келтірілген жүйе берілсін:

және оның алғашқы жуықтаулары белгілі болсын. Әдістің негізгі идеясы белгісіздің (k+1) – ші жуықтауын есептегенде, оның алдында есептелген белгісіздердің (k+1) - ші жуықтауы қолданылады.

Итерациялық схеманың түрі мынадай болады:

Айталық болсын, мұнда

; .

Онда Зейдель процессін матрицалық түрде былай жазуға болады:

.

4.5.4 Зейдель процессінің жинақтылығының жеткілікті шарты

Теорема 4.Егер сызықтық жүйе

(3.5.11)

үшін шарты орындалса, онда осы жүйеге арналған Зейдель процессі кез-келген алғашқы вектор үшін жүйенің жаңғыз шешіміне жинақты болады.

Дәлелдеуі:

. (3.5.12)

мөлшері үшін процестің жинақтылығын қарастырайық. k – шы жуықтау үшін

. (3.5.13)

Дәл шешімнен (3.5.13) алып тастайық

. (3.5.14)

векторының i-ші компоненті үшін (4.3.14) аламыз

.

Осы жерден:

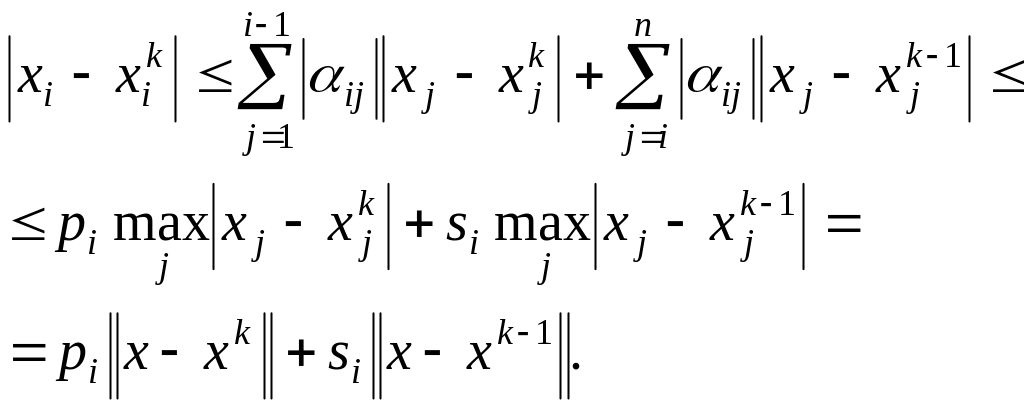(3.5.15)

Себебі (3.5.15) кез-келген үшін орынды, онда ол үшін де орынды. Сонда:

.

Демек, (3.5.15)-тен аламыз:

, (3.5.16)

мұнда .

Осылайша (3.5.16)-дан аламыз:

. (3.5.17)

-ді бағалаймыз. екенін көрсетейік.

болғандықтан, онда .

Демек:

.

(3.5.17)-ден аламыз:

.

Егер . Дәлелдеу керек осы еді.