Приведенный водяной эквивалент потоков W определяется из уравнения

тг⁼ У^(1Х'¹⁰⁾

5. Передача тепла через стенку

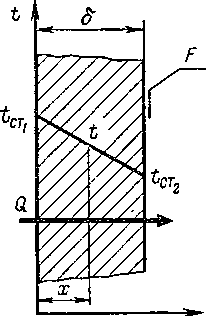
Передача тепла через плоскую стенку теплопроводностью.

Через плоскую однородную стенку поверхностью F и толщи-

ной б (рис. IX-4) тепло Q передается тепло- проводностью. Коэффициент теплопроводности материала стенки равен X. Согласно закону Фурье, можно записать:

Q^-X-^F dx

или для плотности теплового потока q = Q/F

. dt

Рис. IX-4. Изменение температуры при теплопроводности

х через плоскую стенку.

Разделив переменные и проинтегрировав, получим

* t

q J dx = —X | dt 0 t_CT

1

qx = X (*_CTl — t) Для всей стенки (x = 6, t = t_cT2), получим

Ф = X (t_CT± — t_{c T2}) Из уравнений (IX,И) и (IX, 12) получим

или

t = t.

ст_х "

^CTj ^с

(IX,И) (IX,12)

(IX,13)

т. е. распределение температур в плоской стенке имеет ли­нейный характер. Плотность теплового потока через плоскую стенку определяется из следующего выражения:

Я — -чт (k_Tl — *ст₂)

(IX,14)

Отношение Х/6 называется тепловой проводимостью стенки, а обратная величина 8/Х— тепловым сопротивлением. Общее количество переданного через плоскую стенку тепла будет равно

Q=qF = -у (^СТ_Х — *ст₂) F

(IX,15)

Передача тепла теплопроводностью через многослойную пло- скую стенку. По аналогии с предыдущим рассмотрим передачу тепла теплопроводностью через плоскую многослойную стенку (рис. IX-5), состоящую из п слоев. Будем считать, что смежные соприкасающиеся поверхности имеют одинаковую температуру. Согласно уравнению (IX, 14), можно записать для каждого слоя

следующие выражения:

^{q =}"б7('^СТ2 7^?СТз)

7Г(*^стя~'^стл+1)

'fr /

Решив эти уравнения относительно разности температур и сложив левые и правые части равенств, получим

i=1

tc

Плотность теплового потока

Я =

^tcrl ~ ^tcTn+1

£ (W

F

(IX,16)

Стоящее в знаменателе выражение 2 (6Л) представляет собой

*=i

общее термическое сопротивление при теплопроводности через

Рис. IX-5. Распределение температур по толщине многослойной стенки при теплопро­водности.

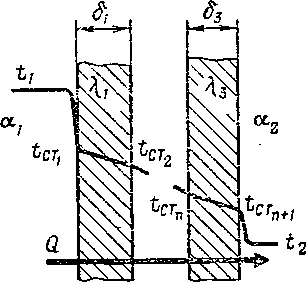
Рис. IX-6. Схема передачи тепла через многослойную плоскую стенку.

многослойную стенку. Температура на границе двух любых со­седних слоев определяется из уравнения

/

*ст_/+1 = — Я 2 1=1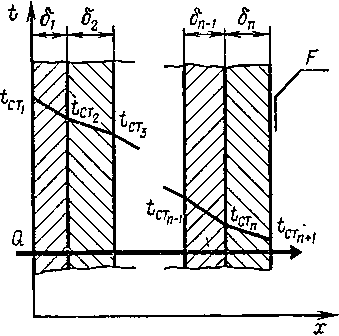

При j = п получим общую разность температур для многослойной стенки t_CTn+1 — f_CTi.

Теплопередача через плоскую многослойную стенку. Горячий поток, имеющий температуру t_l9 омывает многослойную стенку (рис. IX-6), изменяя температуру в прилегающем к стенке слое от t_x до t_c._г . Далее по толщине стенки температура изменяется от t^ до Кт_п+1 ^{и в слое} холодного потока вблизи стенки — от t_CTn+1 до /₂. От горячего потока к стенке и от стенки к менее горячему потоку тепло передается конвекцией, а внутри стенки — теплопроводностью. Поскольку плотность теплового потока через разные участки одинакова, можно записать следующие уравнения:

? ⁼ (^1 ~ Ч+l)

i=1

1-У

где а^ и а₂ — коэффициенты теплоотдачи от горячего потока к стенке и от стенки к нагреваемому потоку соответственно.

Определив из приведенных уравнений разности температур для соответствующих участков и сложив правые и левые части этих выражений, получим

К «1

i=1

Между тем, из уравнения (IX,4) следует, что

Отсюда

t -t -J- h h - _к

l l , v ^б/

⁺ 2ir⁺i ^(IX'¹⁷⁾

т. е. общее термическое сопротивление 1 /К равно сумме всех частных термических сопротивлений. Уравнение (IX, 17) служит для расчета коэффициента теплопередачи

Из уравнения (IX,17) следует, что 1/К > 1/а_ъ 1/К > бД_г и 1/К > 1/а₂, т. е. К < а _1? /С < V6_£- и /С < а₂. Следовательно, коэффициент теплопередачи К всегда меньше каждого из коэффи­циентов теплоотдачи а_ь а₂ и тепловой проводимости Я/б любого слоя стенки.

Передача тепла через цилиндрическую стенку теплопровод­ностью. Рассмотрим теплопроводность однородной цилиндриче­ской стенки (стенки трубы) внутренним диаметром d_B = 2г_в и наружным d_n = 2г_я, длина которой / (рис. IX-7).

Разделим переменные и проинтегрируем

Q dr_

2Ш ' г

j ^dt=—ш

^CTi

t — t, радиуса. При г• = rH t = tcТ2, и из уравнения (IX, 18) получим следующее выражение для разности температур стенки Q 1п гн 2пЫ гв При направлении теплового потока снаружи трубы внутрь урав- нение Фурье можно записать в виде (рис. IX-7, б) dx где г = гн — х, если х = 0, г = гн; при х = rH = rB, г = гв. После преоб- разований получим выражение Q d (гн —х) Q dr 2лЫ ' гн—х ~~ 2лк1 " г Согласно закону Фурье, для любой изотермической поверх- ности радиусом г можно записать следующее выражение: Q=—X^2nrt dr tt или ст-£ : 2nKl г (IX,18) Из полученного выражения следует, что по толщине стенки температура изменяется по логарифмическому закону. Это свя­зано с изменением плотности теплового потока при изменении 1 Гн				11		1 К
с Гй x	s j j j		п>
^сг,	V
		/V// V//					\\Vfc
	1	/у/,							1
а					tcrz
		'//л
г					г		N > >		X

Рл2. IX-7. Изменение температуры при теплопроводности через цилиндрическую стенку: а — греющий поток внутри трубы; б — то же, снаружи трубы.

^ст. " tc

(IX,19)

Проинтегрируем это уравнение в пределах от t и от г = г_н до г справа, получим

t f ^Q In ^r

При г = г_в и f = £_СТг получим уравнение (IX, 19).

Теплопроводность многослойной цилиндрической стенки. Урав- нение (IX, 19) можно применить к каждому слою многослойной цилиндрической стенки

q ^ги

/ / Q _ln Ч

^{2 3}

'п+1' 2кХ_п1 г,

^СТ_Г . - ~ 'ТГ-Z Г In

У J-ln-^

Это количество тепла может быть отнесено к некоторой поверх-

ности F = 2л;/г, тогда

F it \

(IX,23)

1=1

за поверхность F может быть принята, например, поверхность внутренняя (г = г_в) или наружная (г = г_н) трубы. С целью упрощения расчетных уравнений для каждого слоя цилиндриче- ской стенки!применяют уравнение (IX, 14) для плоской стенки, в котором\F = F_t. Величину F_£ рассчитывают как среднюю логарифмическую

F_H. — F_B.

или

_г. = (IX,25)

¹ 1п (_Ч./_Ч.)

= t_CTl до t слева (IX,20)

'Л

Сложив левые и правые части этих уравнений, получим

1 L

1=1

Откуда количество переданного тепла Q равно

Q = (IX,22)

i=i

^F (^tc4 ~ *^CTn+i)

hFi 1
1 6;	. 1