§ 2. Риск и способы его снижения.

Страхование

В условиях асимметричности информации и неопреде-

ленности люди в осуществлении своей экономической деятельности неизбежно идут на риск. Под риском понимается ситуация, когда, зная вероятность каждого возможного исхода, все же нельзя точно предсказать конечный результат. Рассмотрим некоторые основные по-

203

Глава 8

нятия, связанные с поведением человека в условиях неопределенно­сти. Участие в лотерее - типичный пример рисковой деятельности.

Ожидаемое значение случайной величины (например, выигрыш или проигрыш в лотерее) подсчитывается по формуле математичес­кого ожидания:

(1) где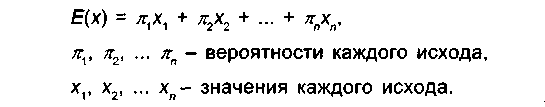

При этом важно учитывать, что вероятности могут иметь различ­ную природу, то есть быть как объективными, так и субъективными. Те ученые, которые придерживаются концепции объективной природы вероятностей, полагают, что значения вероятностей потенциально оп­ределимы на математической основе. Так, французский астроном, ма­тематик и физик Пьер Лаплас определял вероятность исследуемого события как отношение количества благоприятных исходов данного со­бытия к количеству всех возможных исходов. Сторонники субъектив­ного подхода (например, американский экономист и статистик Леонард Сэвидж) полагали, что вероятности - это степени убежденности в на­ступлении тех или иных событий.

В любом случае, какую бы трактовку природы вероятностей мы ни приняли, нам важно различать математическое ожидание (предпола­гаемое значение исхода) и ожидаемую полезность.

Истоки математического обоснования теории ожидаемой полез­ ности можно встретить в работах швейцарских математиков Габриэля Крамера и Даниила Бернулли, последний из которых предложил свое решение знаменитого Санкт-Петербургского парадокса.¹ Парадокс формулируется следующим образом: индивиды готовы заплатить все­ го лишь небольшую сумму денег за участие в игре, в которой матема­ тическое ожидание выигрыша бесконечно велико. Игра заключается в подбрасывании монеты до тех пор, пока не выпадет заданная ее сто­ рона, например, «орел», а размер выигрыша определяется количе­ ством подбрасываний монеты до выпа­ дения заданной стороны. На этом игра

заканчивается. Так, при первом подбра- ' Даниил Бернулли (1700-

сывании в случае выпадения «орла» 1782), швейцарский математик субъект X выплачивает субъекту У 1 и естествоиспытатель. В 1723- долл.; во втором таком же случае У по- ^{1725 гг} Работал в Петербургс- о . кой Академии наук на кафедрах

лучит 2 долл. в третьем - 4 долл., т. е. . '

физиологии и математики.

за каждый бросок с выпадением «орла» Габриэль Крамер (1704-

субъект X выплачивает при п-ом броске 1752) - швейцарский матема- 2 долл. тик.

204

Экономика неопределенности

Вероятность (ж) выигрыша в игре с подбрасыванием монеты, со­гласно теории вероятности, составляет 50%, или 0,5 при каждом броске.

Математическое ожидание денежного выигрыша при первом брос­ке составляет ж х 1 долл. или 0,5 х 1 долл. = 0,5 долл. При втором броске оно составит (0,5 х 0,5) х 2 долл. = 0,5 долл. Общее ожидае­мое значение представляет собой сумму ожиданий на каждой стадии игры и составит, следовательно, 0,5 долл. + 0,5 долл. + 0,5 долл. + ... Сумма этого бесконечного ряда представляет бесконечно большую величину.

Таким образом, как отмечалось выше, парадокс заключается в том, что ожидаемый денежный выигрыш в такой игре бесконечен, однако большинство людей уклонится от участия в ней.¹ Почему же так происходит? Чтобы объяснить Санкт-Петербургский парадокс, Д. Бернулли предположил, что в данном случае индивиды стремят­ся к максимизации не ожидаемого денежного выигрыша, а мо­рального ожидания, впоследствии названного ожидаемой полез­ностью выигрыша. А это не одно и то же. Рассмотрим эту проблему подробнее в связи с отношением людей к риску.

Идеи Д. Бернулли получили развитие в работах американских эко­номистов Джона фон Неймана и Оскара Моргенштерна, которых часто называют основоположниками теории ожидаемой полезности. Они по­казали, что в условиях неполной информации рациональным выбором индивида будет выбор с максимальной ожидаемой полезностью. Ожидаемая полезность каждого варианта подсчитывается следующим образом:

(2)

Т(

Людям свойственно различное отношение к риску. В экономичес­кой теории принято выделять:

а) нейтральных к риску;

б) любителей риска;

в) испытывающих антипатию к

риску, ИЛИ противников риска. ' См. подробнее: Бернулли Д.

Опыт новой теории измерения

В некоторых случаях математичес- _{жребия в книге}Г_Твория ,Г_отре_

кое ожидание при осуществлении рис- бительского поведения и соро­ковой деятельности может быть равно в са. СПб. 1993. С. 23.

205