Графическая схема общего приема решения математических задач
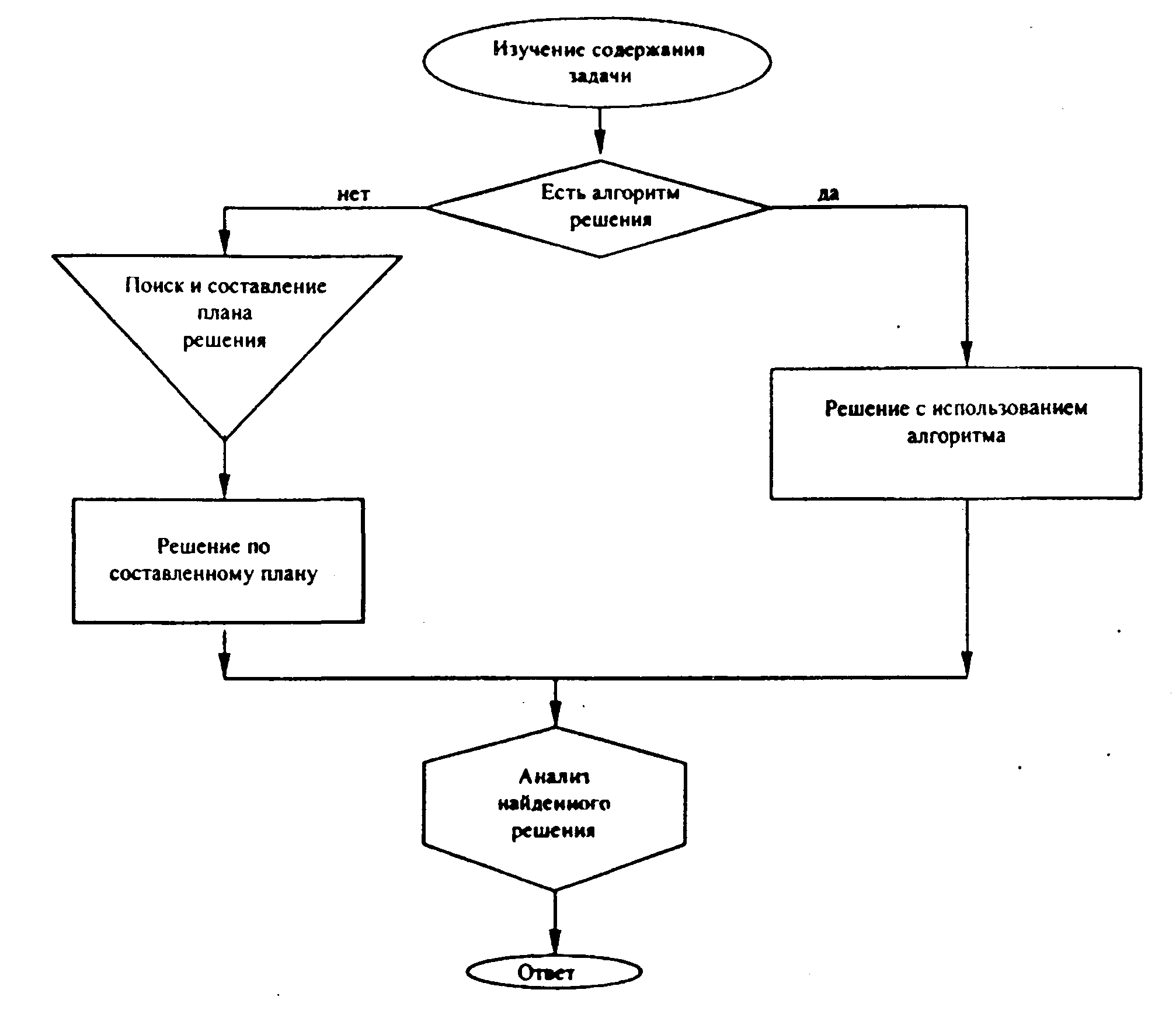
Рис 1.
Основные типы учебных задач являются общими для всех содержательно-методических линий и показаны в п. 1.4.3. данной лекции; студенту необходимо научиться самостоятельно конструировать их примеры на конкретном содержании; примеры специальных учебных задач приводятся в лекции.
5) В последнем пункте рассматриваются специальные методы и приемы обучения, методико-технологические цепочки, о которых говорилось выше; при этом в первую часть этого пункта иногда включаются такие цепочки, которые можно использовать для изучения отдельных тем или разделов, во вторую – на протяжении всей содержательно-методической линии. Приводится анализ типичных ошибок учащихся.
Лекция II. Числа и вычисления
2.1. Логико-математический анализ числовой линии
2.1.1. Число – одно из первых и основных понятий математики как с исторической, так и логической точки зрения, неотъемлемый инструмент современной цивилизации и поэтому – основное понятие образовательной области “Математика” в школе. Зародившись в глубокой древности, оно постепенно, благодаря долгой и упорной психологически трудной работе человека, в течение тысячелетий развивалось – и обобщалось, и развитие понятия числа в сознании учащихся в некоторой степени повторяет этот путь. Поэтому нам важно знать этапы и трудности этого исторического развития; основные из них можно представить следующим образом:
1) Переход (еще в эпоху палеолита) от частных представлений о количестве предметов к представлениям общего характера, для чего нужно было подметить общие признаки отдельных предметов, увидеть их группы. Тогда, по-видимому, в сознании человека возникли представления "один" и "много".
2) Постепенное создание в процессе наблюдений понятия о первых числах натурального ряда; при этом понятию о числе отвлеченном всегда предшествовало и сначала с ним совпадало понятие о числе каких-нибудь определенных предметов, что выражалось в соответствующих числовых терминах (названия "луна", "я" для числа "один", "глаза", "уши" для числа "два" и т.д.).
3) Долгий и трудный переход, связанный с развитием ремесел и торговли, от понятия о числе определенных предметов к числу отвлеченному, постепенное, с использованием пальцев рук и затем ног, удлинение счета.
4) Возникновение из операции счета и идеи порядка в сознании людей представления о натуральном ряде чисел, продолженном достаточно далеко; это нашло отражение в трудах античных ученых.
5) Постепенное рождение в течение столетий и под влиянием человеческой деятельности идеи о действиях над натуральными числами.
6) Постепенное приобретение навыков счета и создание практических правил, которые с течением времени распространялись на все большие числа и становились все более точными.
7) Систематизация знаний о числе и создание одной из древнейших наук – арифметики, с развитием которой развивается и само понятие числа.
8) В III в. до н.э. греческий математик Евклид определил число как множество, составленное из единиц. Следуя Евклиду, так же определял число создатель первого учебника арифметики в России Л.Ф. Магницкий (1703 г.). Но еще до XVIII в. применение этого определения встретилось с рядом трудностей: так, из него следовало, что 0 и 1 не являются числами, с ним не мирилось определение дроби как числа, которое появилось в Древней Греции вслед за расширенным натуральным рядом, не говоря уже об отрицательных и иррациональных числах. Открытие пифагорейцами существования несоизмеримых отрезков, лишенных числового образа, привело их к такой растерянности, что их союз распался. Поэтому вводятся в употребление новые определения отрицательных чисел (XVII в., французский ученый Р. Декарт), иррациональных чисел.
9) Во второй половине XVIII в. завоевывает место более общее определение числа, данное английским ученым И. Ньютоном: число есть отношение одной величины к другой того же рода, принятой за единицу, которое делает равноправными натуральные, целые, дробные и иррациональные числа. Изучение понятия непрерывности привело к уточнению понятия иррационального числа (немецкие ученые Дедекинд, Г. Кантор, К. Вейерштрасс), развитие теории алгебраических уравнений привело к введению понятия комплексного числа.
10) В середине XIX в., в связи с развитием аксиоматического метода в математике и разработкой основ математического анализа немецким математиком Г. Кантором было дано обоснование понятия натурального числа на основании понятия множеств и их равномощности. Другое понятие натурального числа было дано итальянским математиком Д. Пеано на основании сформулированных им аксиом.
11) Таким образом, первое числовое множество – множество N натуральных чисел – может быть построено чисто дедуктивным путем на основе системы аксиом Д. Пеано. Дальнейшее обобщение понятия числа и развертывание учения о числе основано на принадлежащей Г. Кантору интуитивной теории множеств и состоит в последовательном расширении множества натуральных чисел N, которое служит фундаментом построения всех других числовых множеств, по следующей схеме: N Z Q R K, где Z – множество целых чисел, Q - рациональных, R – действительных. К – комплексных, причем на этом современное учение о числе не заканчивается. Следует заметить, что эта схема отличается от исторической (в которой после, натуральных чисел возникли положительные дроби, а уж потом – отрицательные числа) и называется иногда "научной" или "логической" схемой расширения (развития) понятия числа.
Это расширение удовлетворяет следующим условиям: если множество А расширяется до множества В, то 1) А есть подмножество В; 2) все операции и отношения элементов из А определены так же и для элементов В, причем их смысл для элементов из А рассматриваемых уже как элементы расширенного множества В, должен совпадать с тем, какой они имели смысл в множестве А до расширения; 3) в В выполнима операция, которая невыполнима или не всегда выполнима в А (в этом условии – основная цель расширения А); 4) расширение В должно быть минимальным среди всех расширений А, удовлетворяющих условиям 1-3. Конструкция расширения числового множества может быть осуществлена различными путями. Одна из идей, лежащих в основе этих конструкций, получила названия теории пар.
Таким образом, каждый вид чисел определяется как элемент соответствующего числового множества, а его свойства следуют из свойств этого множества. В этой связи существенным являются свойства этих множеств по отношению к таким понятиям, как замкнутость (множество целых чисел является кольцом, а каждое из остальных – полем), упорядоченность, дискретность, счетность, плотность, непрерывность. Кроме того, отдельными самостоятельными разделами теории чисел являются: теория делимости, теория сравнений, алгебраические и трансцендентные числа, числовые функции (см. учебники или лекции по курсам "Числовые системы", "Теория чисел").
2.1.2. Параллельно с развитием понятия числа, под воздействием потребностей практической деятельности людей и самой математики, развивалась техника выполнения операций над числами ("счета"), направленная на рационализацию вычислений и выработку культуры вычислений. Это – совершенствование и систематизация правил, приемов и видов вычислений, конструирование средств вычислений.
Правила вычислений являются следствием определений этих операций и их свойств, а из них следуют приемы вычислений, которые имеют свои отличительные особенности для каждого вида вычислений. Основными видами вычислений являются: письменные вычисления, устные вычисления ("устный счет"), вычисления с помощью различных вспомогательных средств. Письменные вычисления предполагают выполнение строго определенных правил, запись данных и постепенную запись получаемых результатов (как промежуточных, так и окончательных). Устные вычисления ведутся без каких-либо записей, для них в истории развития арифметики накоплено много оригинальных приемов, дающих большой простор для наблюдательности и изобретательности. Средства вычислений, постепенно изобретаемые человеком для их механизации, это – таблицы, графики, разнообразные приборы и машины (счеты, палочки Непера, счетные линейки, арифмометр и другие механические "вычислительные машины", наконец, ЭВТ). Основной критерий возможности применения средств вычислений (в настоящее время и в применении ЭВМ в любой человеческой деятельности) – формулировка алгоритма этой деятельности.
Таким образом, с вычислениями тесно связано понятие алгоритма – точного предписания о выполнении в определенном порядке некоторой системы операций, позволяющих решать совокупность задач определенного класса. Слово “алгоритм” (алгорифм) возникло в результате искажения имени великого узбекского математика IX в. аль-Хорезми. Простейшими алгоритмами служат правила выполнения арифметических действий, знаменитый алгоритм Евклида, вычисления определителей и ранга матриц и т.д., алгоритмы широко используются и в других областях математики, методы которой носят алгоритмический характер. Важность нахождения различных алгоритмов, доказательства их отсутствия для ряда задач и создание общей теории алгоритмов повысилась в связи с бурным развитием программирования, в основе которого лежит понятие алгоритма, информатики и машинной математики. Необходимой частью каждого вычисления является вопрос о точности полученного результата. В связи с этим, а также с тем, что на практике человек в большинстве случаев имеет дело с приближенным характером большинства чисел, сложились понятия точных и приближенных вычислений, а затем и теория приближенных вычислений (связанная с именами российских математиков В.М. Брадиса и А.Н. Крылова). Основными понятиями этой теории являются: абсолютная и относительная погрешность приближения, точность приближения, стандартный вид приближенного значения числа, верные и значащие цифры приближенного значения числа. Основные правила приближенных вычислений связаны с округлением чисел, прикидкой результата действий и оценкой погрешности вычислений [см. 3, гл. XIII, § 4, 5 и учебники информатики – теорию алгоритмов].
2.1.3. В самом общем виде арифметическая задача – это всякий вопрос, для ответа на который нужно по двум или нескольким числам найти новое число. На протяжении всей истории развития арифметики важное место в ней занимают так называемые "чисто арифметические задачи" (задачи, решаемые с помощью четырех арифметических действий без применения алгебры). Существует множество классификаций таких задач – по типам, по числу действий, по содержанию и другие, для которых еще с древности было придумано множество методов решения. Несколько упрощая это множество, можно рассмотреть следующую классификацию.
1) Задачи-примеры, в записи условий которых используются только математические символы (цифры, знаки действий, скобки), а словесный текст, как правило, отсутствует. Метод их решения – выполнение арифметических действий с учетом правила об их порядке.
2) Задачи-расчеты – задачи межпредметного и прикладного характера, иногда с готовой формулой расчета. После составления числового выражения приводятся к задаче-примеру и решаются тем же методом. Например, задача-расчет регионального содержания: "Среди зарегистрированных в 1997 г. в г. Тобольске выбросов, загрязняющих атмосферу, на твердые вещества приходится 1 878 тыс. тонн, а газообразные и жидкие вещества составили на 4 307 тонн больше. Сколько всего выбросов зарегистрировано?"
3) Текстовые сюжетные задачи более сложного математического характера, которые в большинстве случаев легко решаются алгебраически, но, если не пользоваться уравнениями, представляющие собой некоторые трудности и требующие для решения определенной сообразительности. Например, типичная задача такого вида: "Имеется 80 одинаковых по виду монет, среди которых 79 одного веса и одна немного более легкая. Как ее выделить, применяя не более четырех взвешиваний?''
Наиболее распространенные методы решения сюжетных задач: 1) метод "отношений и пропорций" (для задач, в которых величины находятся в прямо и обратно пропорциональной зависимости); 2) метод "введения условной единицы" (для задач на нахождение двух или более чисел по данной их сумме и отношению); этим же методом решаются задачи "на совместную работу", "на бассейны" и т.п.; 3) метод решения задач "на проценты" – нахождение процентов данного числа, числа по его проценту и процентного отношения чисел; 4) метод среднего арифметического (для задач отыскания среднего значения двух или нескольких величин, задач “на смешение”); 5) метод разностного сравнения (для нахождения чисел по их сумме и разности); 6) метод уравнивая данных (для задач, в которых можно исключить одно искомое уравниванием данных); 7) метод проб (испытаний) и другие.