Лекция III. Выражения и их преобразования

3.1. Логико-математический анализ линии тождественных преобразований выражений

3.1.1. История развития алгебры свидетельствует о том, что введение буквенной символики – трудный и длительный процесс. Если первые шаги в этом сделаны, по-видимому, в III в. н. э. (Диофант из Александрии), то существенные достижения относятся ко второй половине XVI в. (Ф.Виет) и к первой половине XVII в. (Р. Декарт); т.е. потребовалось около тринадцати столетий, чтобы проблема получила удовлетворительное решение. Вначале буквы использовали для обозначения неизвестных чисел, которые необходимо найти при заданных условиях; это сравнительно нетрудно. Более трудным шагом стало то, что под буквой можно подразумевать любое число из некоторого множества чисел; это потребовало более высокой ступени абстракции, и поэтому произошло только во второй половине XVI в.

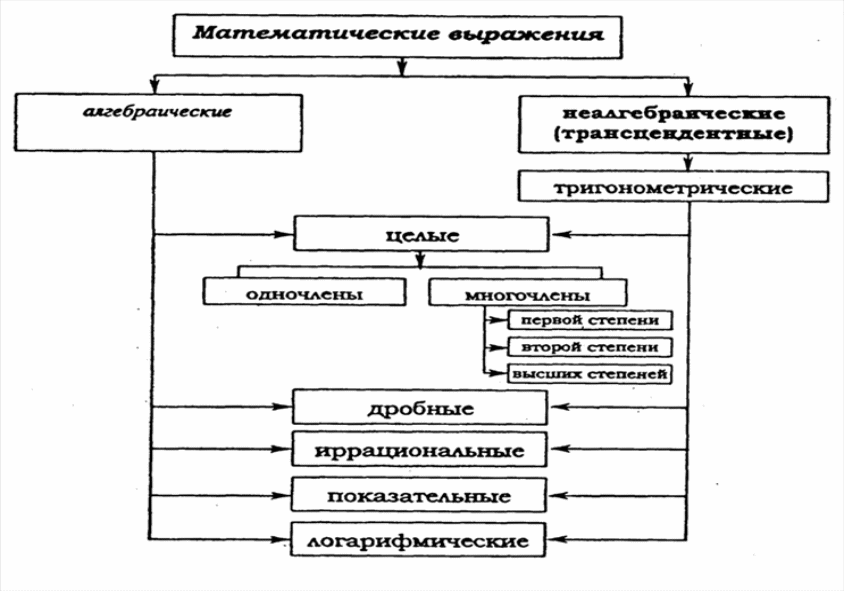
Тождественные преобразования выражений с переменными – одна из основных задач элементарной алгебры, результаты решения которой служат сред­ством решения уравнений и неравенств, рационализации вычислений и других. Основными понятиями данной содержательно-методической линии являются понятия: "выражение", "тождественно равные выражения", "тождество" и "тождественное преобразование выражения". Выражением в математике называют запись, состоящую из чисел, букв (обозначающих постоянные или переменные величины), знаков математических действий. В числовых множествах имеют дело с числовыми выражениями (не содержащими переменных). В табл. 6 показана классификация основных выражений с переменными.

Для каждого вида выражения существуют подвиды и простейшее или выражение стандартного вида. Значения переменных, при которых выражение имеет смысл, называются допустимыми значениями переменных и образуют область определения выражения. Два выражения называются тождественно равными, если они принимают одинаковые числовые значения при подстановке соответственно равных числовых значений входящих в них букв из общей области определения. Тождеством называется равенство двух тождественно равных выражений. Тождественным преобразованием выражения называется замена одного выражения другим, тождественно ему равным выражением (как правило, более простым вплоть до выражения стандартного вида). Эта замена производится с помощью действий над выражениями, во многом аналогичных действиям над соответствующими видами чисел. При этом результат действия должен быть выражением того же вида, поэтому некоторые действия не выполнимы или не всегда выполнимы в множестве выражений данного вида (например, сложение и вычитание одночленов, деление многочленов). В табл. 7 систематизированы тождественные преобразования выражений, изучаемые в школьном курсе алгебры и начал анализа.

Таблица 6

3.1.2. Тождественные преобразования 1) иррациональных выражений, 2) Первая связана с тем, что каждое из названных выше выражений может быть целым и дробным, тригонометрические выражения – ещё и иррациональным. Поэтому для их тождественных преобразований используются не только основные свойства простейших видов этих выражений и соответствующие формулы (назовём их специальными тождественными преобразованиями), но и тождественные преобразования целых и дробных выражений (назовём их в данном случае общими). Вторая особенность следует из первой и относится к области определения выражения. Целые алгебраические выражения (одночлен и многочлен) определены на всём множестве действительных чисел, но уже область определения дробного алгебраического выражения получается исключением из множества действительных чисел тех значений переменной, которые обращают знаменатель в нуль. Каждый из названных выше видов выражений имеет свою область определения, связанную с областью определения соответствующей функции. Если это выражение целое, то этого условия достаточно, но если дробное – необходимо учитывать область определения дробного выражения и рассматривать условия совместно.

Таблица 7

	Вид выражения	Основные преобразования	Основания для преобразований	Ограничения и дополнительные условия	Вспомогательные и дополнительные преобразования
1	Одночлен	Умножение, возведение в степень, деление одночленов.	Определение одночлена, понятие и свойства степени	Для деления: а) показатель степени переменной делимого не меньше показателя степени той же переменной делителя; б) делитель не содержит переменных, которых нет в делимом.
2	Многочлен	Сложение, вычитание, умножение, деление, возведение в степень, разложение на множители многочленов.	Определение многочлена, распределительный закон умножения относительно сложения, деление суммы на число, понятие степени.	Для деления: степень делимого не меньше степени делителя; деление без ос татка или с остатком.	Приведение подобных слагаемых, раскрытие скобок. Умножение и деление по формулам сокращенного умножения, деление на основе разложения на множители. Возведение в степень двучлена по формуле бинома Ньютона. Выделение полного квадрата в квадратном трехчлене.
3	Дробное выражение	Сложение, вычитание, умножение, деление, возведение в степень дробных выражений.	Определение дробного выражения, осн. свойство дроби, правила действий с числовыми дробями.	Область определения дробного выражения с переменной.	Приведение дробей к общему знаменателю, сокращение дробей.
4	Иррациональные выражения	Умножение, деление, возведение в степень корней извлечение корня из произведения, дроби, степени, корня.	Определение корня, основное свойство корня, теоремы о преобразованиях корней.	Определение арифметического корня, область определения иррационального выражения.	Сокращение показателей корня и подкоренного выражения, вынесение и внесение рационального множителя под знак радикала, уничтожение иррациональности в дроби.
5	Логарифмические выражения	Нахождение логарифма выражения нахождение выражение по его логарифму.	Определение логарифма, основное логарифмическое тождество, теоремы о логарифмировании.	Область определения логарифмического выражения.	Логарифмирование и потенцирование.
6	Тригонометрические выражения	Алгебраические преобразования рациональных и иррациональных тригонометрических выражений.	Правила тождественных преобразований рациональных и иррациональных выражений.	Область определения тригонометрических функций	Преобразования тригонометрических выражений по формулам тригонометрии.