Глава 7 изгиб прямых брусьев

7.1. Общие понятия о деформации изгиба

Изгиб представляет собой такую деформацию, при которой в поперечных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

Изгиб называется чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

В случае, когда в поперечном сечении наряду с изгибающим моментом возникает поперечная сила, изгиб называется поперечным.

Если плоскость действия сил (силовая плоскость) проходит через одну из главных центральных осей инерции поперечного сечения стержня, изгиб называется простым или плоским (применяется также название прямой изгиб).

7.2. Определение внутренних усилий при плоском изгибе

На основании метода сечений можно записать, что:

а) поперечная сила Q в любом произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих по одну сторону от сечения на нормаль к продольной оси балки (ось Y):

( 7.1)

б) изгибающий момент в любом произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно центра тяжести данного сечения:

( 7.2)

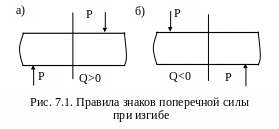
7.3. Правило знаков для изгибающих моментов и поперечных сил

Поперечная сила считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз (рис. 7.1, а), и отрицательной – в противоположном случае (рис. 7.1, б).

Изгибающий момент в сечении балки считается положительным, если нижние волокна растягиваются, а верхние сжимаются (рис. 7.2, а), и отрицательным – верхние растягиваются, а нижние сжимаются (рис. 7.2, б)

Из рис. 7.2 следует более удобное для запоминания правило знаков изгибающих моментов. Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз (рис. 7.2, а) и наоборот.

7.4. Построение эпюр поперечных сил и изгибающих моментов

Построение эпюр Q и М выполняют в следующем порядке.

7.4.1. Определяют опорные реакции с помощью уравнений статики, например:

(7.3)

где Z – ось балки; А, В – любые точки, лежащие на оси Z.

7.4.2. Балка разбивается на n участков. Границами участков будут сечения, в которых меняется характер нагрузки. Это сечения, где приложена сосредоточенная сила, пара сил, начинается или заканчивается распределённая нагрузка.

7.4.3. Для каждого участка по формулам (7.1) и (7.2) составляют в общем виде выражения Q и М в зависимости от текущей координаты Z.

7.4.4. Для характерных сечений определяют значения Q и М. Эта операция может быть выполнена без составления выражений (7.1), (7.2). В этом случае для построения эпюр Q и М используют правила контроля эпюр, основанные на дифференциальных зависимостях:

(7.4)

7.4.5. С помощью значений Q и М, полученных в п. 7.4.4, строят эпюры этих усилий.