§ 1.3. Фізичні співвідношення (узагальнений закон Гука) та основні рівняння теорії пружності

Наведені вище співвідношення з теорії напружень та теорії деформацій справедливі для довільних твердих тіл. Для розрахунку напружено-деформованого стану тіл, що виготовлені із заданого матеріалу необхідно врахувати їх особливі фізико-механічні характеристики. Додаткові рівняння, які отримують шляхом проведення відповідних експериментальних механічних досліджень над зразками із даного матеріалу, називають фізичними співвідношеннями. Такі співвідношення при деформуванні матеріалів у межах пружності носять назву узагальненого закону Гука.

Закон Гука. Напруження та деформації при пружному деформуванні задовольняють співвідношенням [1]

(1.13)

де Е – модуль Юнга, G – модуль зсуву, коефіцієнт Пуассона, які визначаються на основі експериментальних досліджень. Ці коефіцієнти зв’язані співвідношенням .

Застосуємо закон Гука для випадку одновісного розтягу стрижня, який розміщений вздовж осі Ох, коли відмінними від нуля будуть тільки напруження . Із співвідношень (1.13) тоді отримуємо

.

Звідси видно, які експерименти необхідно провести, щоби встановити пружні сталі. Зокрема, коефіцієнт Пуассона (за абсолютною величиною) дорівнює відношення поперечної деформації до поздовжньої при розтязі стрижня.

Узагальнений закон Гука (1.13) дає можливість визначити деформації при відомих напруженнях. Розглянемо випадок, коли відомі деформації. Тоді розглядаючи (1.11) як систему рівнянь відносно напружень, отримуємо

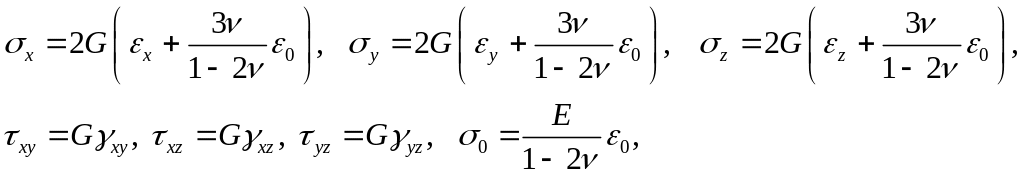(1.14)

де - середні напруження та деформації.

Основні рівняння теорії пружності. Підставляючи вирази для напружень (1.14), у яких деформації визначені через переміщення згідно співвідношень Коші (1.10), у рівняння рівноваги (1.7), отримують систему рівнянь теорії пружності в переміщеннях Ляме [2,6]

(1.15)

де , - оператор Лапласа, (X,Y,Z) – вектор масових сил.

У другому варіанті побудови основних рівнянь використовують рівняння рівноваги (1.7) та рівняння сумісності деформацій (1.12), в яких деформації виражають через напруження згідно закону Гука (1.13) . В результаті отримують 6 рівнянь відносно напружень, які носять назву рівнянь Бельтрамі-Мітчелла [2,6]

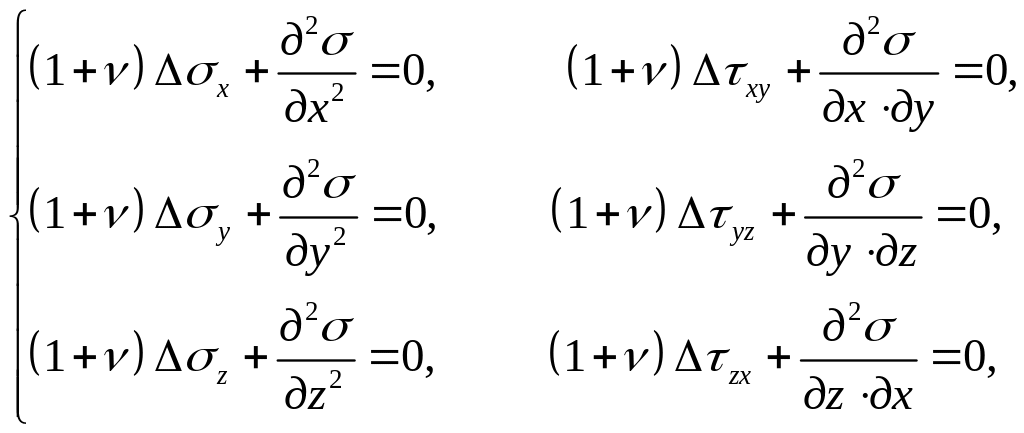(1.14)

де .

До рівнянь (1.13) або (1.14) необхідно додати умови на границі тіла.

Граничні умови. Приймемо, що границею тіла є поверхня S, на якій задано вектор зусиль . Тоді на границі необхідно забезпечити виконання умов, які випливають із формул (1.2)

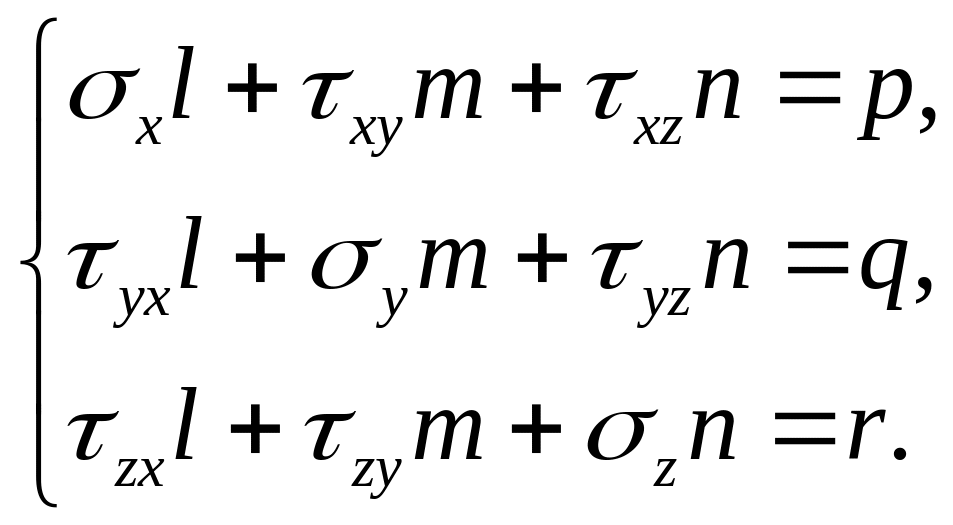(1.15)

Повна система рівнянь, яка доповнена граничними умовами (1.15) називають першою основною задачею.

Друга основна задача має місце, коли в процесі навантаження відомі зміщення всіх точок границі тіла, які позначимо через , що залежать від координат. Тоді умови на границі для такої задачі будуть мати вигляд

. (1.16)

Задачу, яка виникає у випадку, коли на частині границі тіла відомі прикладені зусилля, а на решті – переміщення, називають змішаною.

І І. ОДНОВИМІРНІ ЗАДАЧІ ТЕОРІЇ ПРУЖНОСТІ

На практиці часто виникають задачі теорії пружності, в яких напруження та перміщення залежать тільки від однієї координати. Такі задачі називають одновимірними.