ВСТУП

Питання, пов'язані з розрахунками на міцність і жорсткість елементів конструкцій, розглядаються в традиційних дисциплінах "Опір матеріалів" і "Будівельна механіка".

Методи опору матеріалів базуються на певних гіпотезах, які з одного боку істотно спрощують процес розрахунків, а з другого, дозволяють отримувати достатньо точні для практики результати стосовно до широкого кола інженерних задач. Однак, в основному, такі підходи можуть бути використані до стрижневих систем.

При розгляді деталей машин і елементів конструкцій, що мають складну геометричну форму, необхідно застосовувати точніші розрахункові методики, які вивчаються в курсі "Теорії пружності".

В математичній лінійній теорії пружності виходять з наступних припущень:

1. Приймається, що матеріал тіла є суцільним, тобто атомно-молекулярна структура матеріалу не враховується.

2. Вважають, що перед навантаженням у тілі напруження і деформації відсутні.

3. Матеріал тіла приймають ідеально пружнім. Тобто, вважають, що форма тіла після його розвантаження не змінюється.

В даному конспекті лекцій компактно викладено основи математичної лінійної теорії пружності та дано їх застосування до дослідження практично важливих задач (пластини, призматичні тіла і ін.).

Для розв’язування типових задач теорії пружності наведено тексти програм на мові "Matlab", за допомогою яких можуть бути безпосередньо виконані розрахунки для конкретних задач при відповідно заданих даних читачем. Зазначимо, що такі розрахунки можуть бути виконані, якщо на комп’ютері встановлена система "Matlab" та до неї під’єднано "MS Word" за допо­могою пакету "NoteBook". Таке під’єднання проводиться із системи "Matlab" використовуючи підказки, які з’являться, якщо набрати в командній стрічці: help Notebоok та натиснути клавішу ''Enter''. Якщо під’єднання проведено правильно, то в головному меню "MS Word" з’явиться додаткове меню "Notebook". Зазначимо, що в електронному вигляді цей конспект в термінах системи "Matlab" називають М–книгою.

І. ОСНОВНІ РІВНЯННЯ ТЕОРІЇ ПРУЖНОСТІ

§ 1.1. Теорія напружень

Зовнішні сили, які діють на тверде тіло, розділяють на поверхневі і об’ємні. Поверхневі сили прикладені до границі тіла. Інтенсивність вектора прикладених зусиль в довільній точці Q границі визначають наступним чином: виділяють область малих розмірів, яка включає точку Q ; знаходять на ній головний вектор прикладених сил і ділять його на площу області.

Об’ємні сили діють у внутрішніх точках тіла. До таких сил належать: сили тяжіння; сили інерції (які, зокрема, виникають при обертовому русі тіла).

В тілі виникають внутрішні сили, які протидіють прикладеному зовнішньому навантаженню. Основна мета теорії пружності полягає в знаходженні внутрішніх сил.

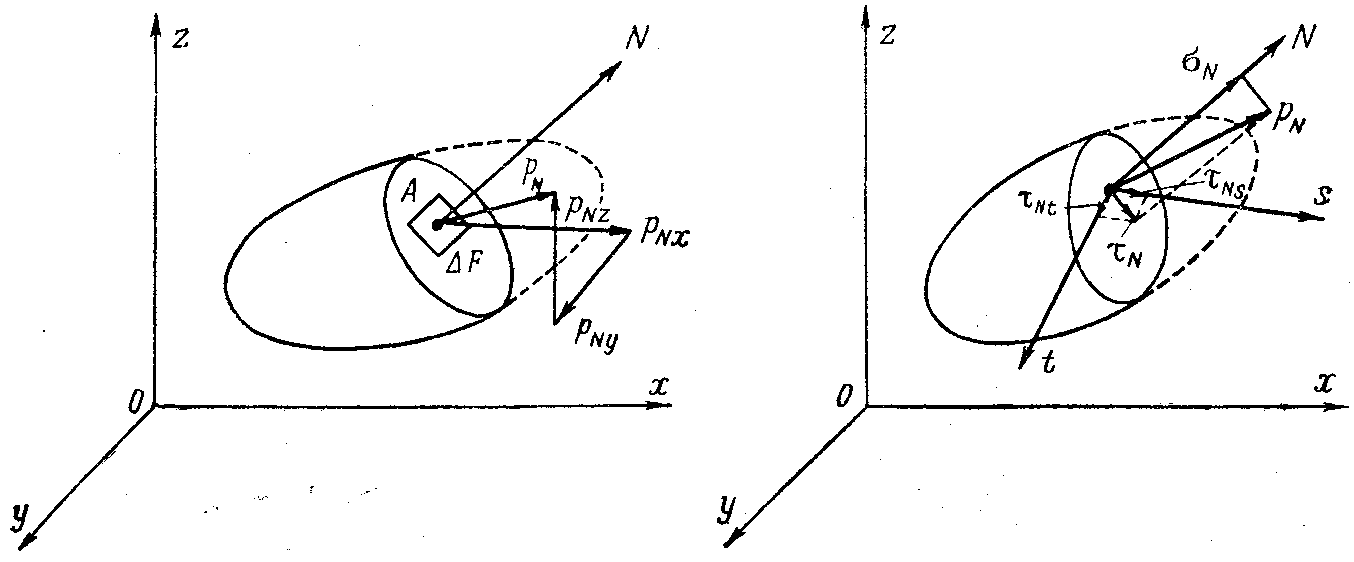
Розглянемо довільну внутрішню точку тіла А і проведемо через неї певний переріз (рис.1). Виділимо в цьому перерізі область малих розмірів, яка включає точку А; знайдемо на ній головний вектор внутрішніх сил і розділимо його на площу області . Отриманий вектор називають вектором напружень в точці А.

А	б

Рис.1.1.

Підкреслимо, що вектор напружень залежить від орієнтації площинки, яку визначають нормаллю .

Віднесемо тіло до декартової системи координат (x,y,z). Розглянемо площинку, перпендикуляром до якої є вісь Ox. Проекції вектора напружень (рис.1.2.а) на цій площинці позначають так: .

Рис.1.2.

Аналогічно, проекції вектора напружень на площинках, перпендикуляром до яких є координатні вісі Oy (рис.1.2.б) і Oz позначають і . Підкреслимо, що перший індекс вказує на розташування площинки, до якої відносяться напруження. Другий індекс в проекціях вказує на напрямок проекції.

Виділимо уявно в тілі паралелепіпед з гранями, які паралельні координатним осям. Введені напруження зображені на рис.1.3.

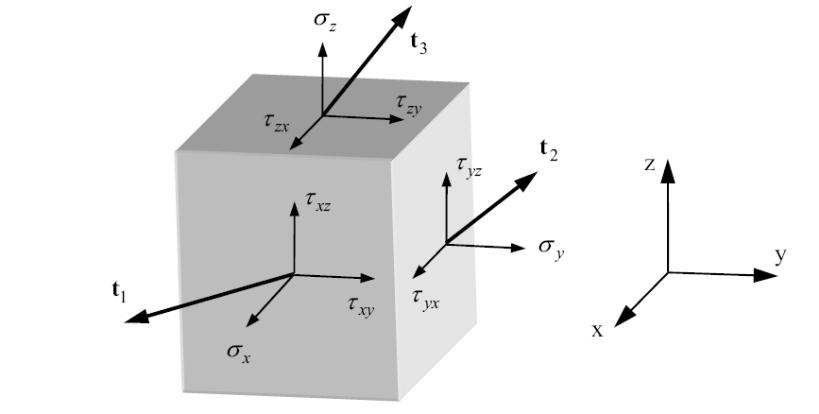
Рис.1.3

Тензор напружень. Таким чином, напружений стан в довільній точці тіла визначають дев’ять компонент тензора напружень

. (1.1)

Зазначимо, що в першому рядку розміщені проекції вектора напружень на площинці, перпендикуляром до якої є вісь Ох. Аналогічно, в другому і третьому рядках розміщені проекції вектора напружень на площинках, перпендикулярами до яких є осі Оy і Oz.

Напруження на нахилених площинках. Вектор напружень на довільній площинці з напрямними косинусами (l, m, n) (рис.1.4) визначається із умови рівноваги елементу .

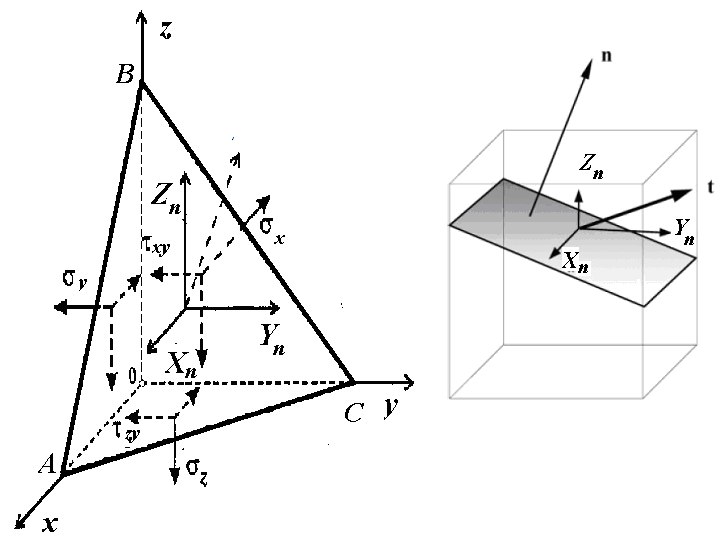
Рис.1.4

Звідси отримуємо формули

, , (1.2)

.

Напруження в повернутих системах координат. Приймемо, що відомі напруження в декартовій системі координат Oxyz – тензор (1.1). Знайдемо напруження в новій декартовій системі координат , яка повернута відносно початкової. Позначимо напрямні косинуси нових осей Ox', Oy', Oz' відносно координатних осей Ox, Oy, Oz через відповідно : ( ), ( ), ( ). Тоді напруження в новій системі координат визначаються за формулами [2]

. (1.3)

Тобто, для знаходження напружень необхідно перемножити три матриці. Перепишемо формулу (1.3) у матричному вигляді

, (1.4)

де

– транспонована матриця N.

Формула (1.4) зручна при обчисленнях, оскільки в сучасних математичних комп’ютерних програмах множення матриць є стандартною процедурою.

На практиці часто виникають випадки коли має місце плоский напружений стан, за якого напруження . Тоді відмінними від нуля будуть тільки напруження . Для визначення напружень у новій системі координат на основі (1.3) отримуємо

, де ,

кут між віссю Ох і нормаллю до площинки n.

Звідси

Головні напруження. Відомо, що в кожній точці тіла існують три взаємно перпендикулярні площинки, на яких дотичні напруження рівні нулю. Ці площинки називають головними, а нормальні напруження на них – головними напруженнями.

Підкреслимо, що на головних площинках вектор напружень напрямлений перпендикулярно до них. Тобто, на головних площинках для вектора напружень справедливі умови , де – невідомий множник, який рівний за величиною головному напруженню. На основі формул (1.2) тоді отримуємо систему алгебраїчних рівнянь [1,2]

(1.5)

Відмінні від нуля розв’язки цієї системи існують, якщо її детермінант рівний нулю. Звідси отримуємо, що головні напруження визначаються з характеристичного рівняння

.