18. Парабола. Каноническое уравнение параболы и его свойства.

19. Гипербола. Каноническое уравнение гиперболы и его свойства.

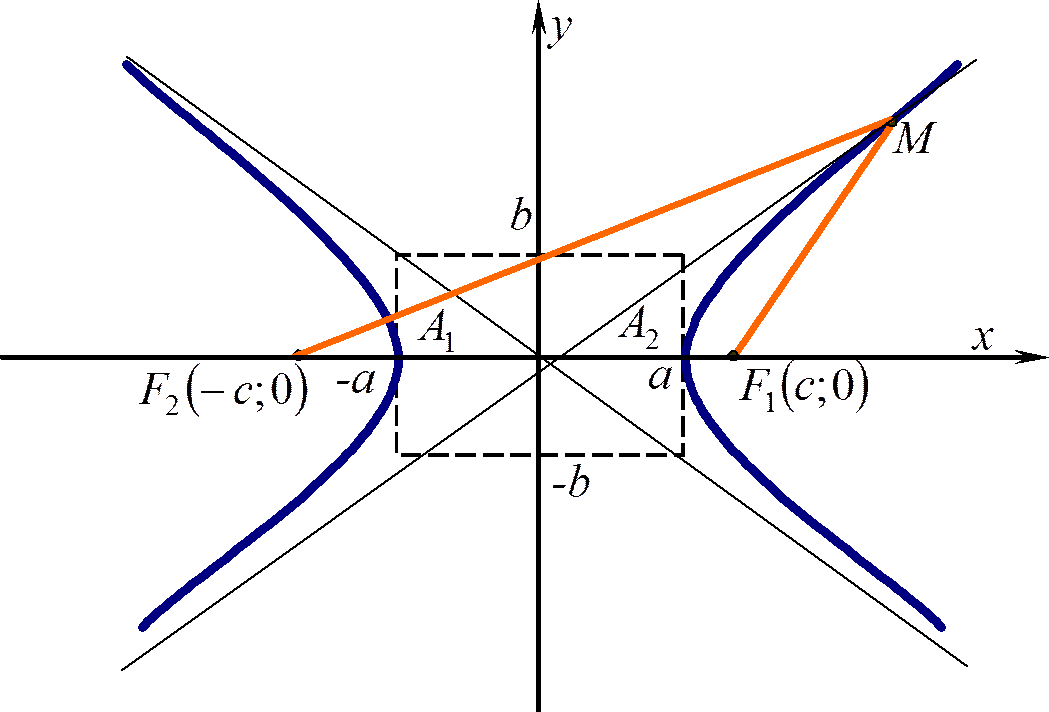
Гиперболой называется геометрическое место точек M, для которых модуль разности расстояний от двух фиксированных точек F1 и F2, называемых фокусами, есть величина постоянная и обозначаемая 2a. R1 - r2 = ±2a (2) r1 = F1M и r2 = F2M называются фокальными радиусами точ- ки M. Расстояние между фокусами обозначается 2c , F1F2 = 2c. Из 4F1F2M следует, что |F1M −F2M| < F1F2, т.е. 2a < 2c. Сле- довательно, для того, чтобы г.м.т. было не пусто, необходимо, чтобы a < c. Выбирая прямоугольную систему координат Oxy как и в слу- чае эллипса, получим каноническое уравнение гиперболы x 2 a 2 − y 2 b 2 = 1, (2k) где b 2 = c 2 − a 2 . Как и в случае эллипса получаем, что гипербола симметрич- на относительно и осей, и начала координат. В первой четверти гипербола является графиком функции y = b a √ x 2 − a 2 , x ≥ a. Очевидно, что если x возрастает от a до ∞, то y возрастает от 0 до ∞, причем прямая y = b a x является асимптотой, т.е. прямой к которой график функции приближается на бесконеч- ности. Таким образом, гипербола имеет две асимптоты y = b a x 97и y = − b a x. Мы получаем форму гиперболы изображенную на рисунке выше. Ось Ox пересекает гиперболу в точках (−a, 0), (a, 0), которые называются ее вершинами. Числа a и b называ- ются полуосями, причем a называется действительной полу- осью, а b — мнимой. Гипербола состоит из двух изолированных кусков, которые называются ее ветвями. Практически гиперболу строят так. Сначала строят так назы- ваемый основной прямоугольник со сторонами x = ±a и y = ±b. Затем проводят прямые, являющиеся продолжениями диагона- лей основного прямоугольника. Это — асимптоты гиперболы. А затем уже рисуют саму гиперболу. Отметим, что уравнение x 2 a 2 − y 2 b 2 = −1 также определяет гипер- болу, которая называется двойственной к гиперболе (2k). Она имеет такие же асимптоты, как и гипербола (2k), и изображена на рисунке пунктиром.

Теорема. (Свойства гиперболы.)

1. В канонической для гиперболы системе координат, в полосе

                                        

нет точек гиперболы.

2. Точки  лежат на гиперболе.

3. Гипербола является кривой, симметричной относительно своих главных осей.

4. Центр гиперболы является его центром симметрии.

   Доказательство. 1, 2) Сразу же следует из канонического уравнениягиперболы.

3, 4) Пусть М(х, у) – произвольная точка гиперболы. Тогда еекоординаты удовлетворяют уравнению (4). Но тогда координаты точек  также удовлетворяют уравнению (4), и, следовательно, являются точками гиперболы, откуда и следуют утверждения теоремы.

Теорема доказана.

20. Окружность, эллипс, гипербола и парабола как алгебраические линии второго порядка и как сечения конуса.

21. Геометрический вектор (длина вектора, нуль-вектор, равенство геометрических векторов, коллинеарность и компланарность). Координатные орты.

Вектор- называется всякая величина, обладающая направлением. Вектор, началом которого служит точка А, а концом точка- В, обозначается АВ.

Длина вектора, также называется модулем. Модуль это скалярная величина, обозначается двумя вертикальными чертами.

Нуль-вектор- это вектор длина которого равна 0.

Равенство векторов- два(ненулевых)вектора а и b равны, если они равнонаправленные и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны. Вектор можно переносить параллельно самому себе , а начало вектора помещать в любую точку О пространства. Равные векторы так же называют свободными.

Коллинеарные – векторы а иb называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают, а||b. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.

Компланарные- три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов, хотя бы один нулевой или два любые коллинеарные, то такие векторы компланарны.

Орт вектор- вектор, длина которого равна единице, называется единичным вектором и обозначается через ē. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора а и обозначается а°.