16. Окружность. Общее и каноническое уравнения окружности.
Определение.Окружностью называется множество, состоящее из всех точек плоскости, находящихся на равном расстоянии R от фиксированной точки С.
Число R – называется радиусом окружности, точкаС–центром.
Воспользуемся
определением окружности для вывода ее
уравнения.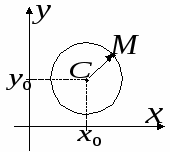
Пусть
точка
–
центр окружности. Точка M(x;y)–
произвольная точка окружности, а радиус
этой окружности равен R.
По определению
,
тогда, используя формулу вычисления
длины вектора
,
имеем
,
тогда
.
Возведем обе части равенства в квадрат.
Тогда уравнение окружности с центром
в точке 
и
радиусом R имеет
вид:
каноническое
уравнение окружности
В
частности, уравнение окружности с
центром в начале координат и
радиусом R имеет
вид: 
.
17. Эллипс. Каноническое уравнение эллипса и его свойства.
Опр: Эллипс – геометрическое место точек в плоскости, сумма расстояния от которых до двух заданных точек в плоскости есть величина постоянная. Заданные точки – фокусы Эллипса.
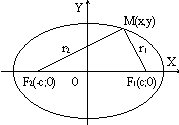
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
.
(4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
.
Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
, 
,
откуда получаем:
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
.
Сокращая, получаем:
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
.
Возводим в квадрат
.
Раскрываем
скобки и сокращаем на 
:
,
откуда получаем:
.
Используя равенство (2), получаем:
.
Разделив
последнее равенство на 
,
получаем равенство (4),
ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
.
Здесь мы воспользовались равенством (2) и (3).
Таким
образом, 
.
Аналогично, 
.
Теперь заметим, что из равенства (4) следует, что
или 
и
т.к. 
,
то отсюда следует неравенство:
.
Отсюда, в свою очередь, следует, что
или 
и
, 
.
(5)
Из
равенств (5) следует, что 
,
т.е. точка М(х, у) является точкой эллипса,
ч.т.д.
Теорема доказана.
С/a= Е(эпсилон) - эксцентриситет Эллипса. Всегда <1, равен нулю когда фокусы совпадают.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координатназывается центром эллипса.
Свойства эллипса.
Теорема. (Свойства эллипса.)
1. В канонической для эллипса системе координат, все
точки эллипса находятся в прямоугольнике
, 
.
2.Точки 
лежат
на
эллипсе.
3. Эллипс является кривой, симметричной относительно
своих главных осей.
4. Центр эллипса является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.
3,
4) Пусть М(х, у) – произвольная точка
эллипса. Тогда ее координатыудовлетворяют
уравнению (4). Но тогда координаты точек 
также
удовлетворяют уравнению (4), и,
следовательно, являются точками эллипса,
откуда и следуют утверждения теоремы.
Теорема доказана