5. Переход от декартовой к полярной системе координат и обратно.

О — полюс, ρ — полярный радиус, φ — полярный угол

Переход от полярной системы координат к декартовой

Если полюс полярной системы координат совместить с началом прямоугольной системы координат, а полярную ось с положительной полуосью Ox, то по известным полярным координатам точки А( ρ; φ) ее прямоугольные координаты вычисляются по формулам:

x1=ρ*cosφ

y1=ρ*sinφ

Переход от декартовой системы координат к полярной

6. Преобразование координат для прямоугольной системы координат методом сдвига и поворота.

Преобразование декартовых прямоугольных координат при параллельном сдвиге осей определяется формулами

х = х'+ а,  у=у'+ b.

Здесь х, у суть координаты произвольной точки М плоскости относительно старых осей, х', у' — координаты той же точки относительно новых осей, а, b — координаты нового начала О' относительно старых осей (говорят также, что а есть величина сдвига в направлении оси абсцисс, b — величина сдвига в направлении оси ординат).

Преобразование декартовых прямоугольных координат при повороте осей на угол  (который надо понимать, как в тригонометрии) определяется формулами

x = х' cos  — y sin ,у = x' sin  — у' cos .

Здесь х, у суть координаты произвольной точки М плоскости относительно старых осей, х’, у’ — координаты той же точки относительно новых осей.

Формулы x = х' cos  — y sin  + а, у = х' sin  + y cos  + b

определяют преобразование координат при параллельном сдвиге системы осей на величину а в направлении Ох, на величину b в направлении Оу и последующем повороте осей на угол .

Все указанные формулы соответствуют преобразованию координат при неизменном масштабе

7. Алгебраическая линия и её порядок. Теорема об инвариантности порядка.

Теорема об инвариантности порядка алгебраической линии

Если в некоторой аффинной системе координат на плоскости линия задана уравнением (3.4), то и в любой другой аффинной системе координат эта линия задается уравнением того же вида (3.4) и той оке степени.

Действительно, пусть в аффинной системе координат  уравнение имеет вид (3.4): Получим уравнение этой линии в другой (новой) аффинной системе координат  . Старые координаты точки связаны с новыми ее координатами выражениями (2.8):

где  — координаты вектора переноса начала координат  , а  — элементы матрицы перехода базиса  к новому . Подставим эти выражения в одночлен  :

Раскрывая скобки, получаем многочлен двух переменных  , степень которого не больше, чем  . Аналогичные многочлены получим из других одночленов, входящих в левую часть (3.4). Сложив эти многочлены, получим многочлен  , степень которого не превосходит степени исходного многочлена  . Таким образом, при замене системы координат порядок алгебраической линии не увеличивается. Но он не может и уменьшиться, так как если порядок уменьшится при переходе к новой системе координат, то он должен увеличиться при обратном переходе к старой системе координат. Следовательно, порядок алгебраической линии остается неизменным в любой аффинной системе координат (говорят, что порядок алгебраической линии является инвариантом). Теорема доказана.

8. Уравнение прямой на плоскости, проходящей через две заданные точки.

9. Уравнение прямой с угловым коэффициентом. Пучок прямых.

10. Уравнение прямой, проходящей через заданную точку в заданном направлении.

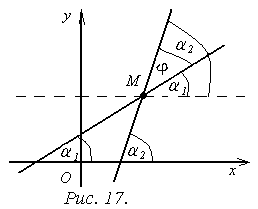
11. Угол между двумя прямыми.

Пусть прямые l₁ и l₂ заданы уравнениями: l₁: y=k₁x+в₁ l₂: y=k₂x+в₂

c углами наклона к оси Ох соответственно φ₁ и φ₂ (рис.2).

Обозначим через φ₁ угол наклона прямой l₁ к оси О_х и через φ угол, на который нужно повернуть прямую l₁до совпадения с l₂ (рис. 6).  Тогда φ₁+φ=φ₂ будет, очевидно, углом наклона прямой l₂ к оси O_х. Отсюда φ=φ₂-φ₁ и если прямые l₁ и l₂ не являются перпендикулярными, то (по известной формуле тригонометрии)

Заметив, что tgφ₁=k₁ и tgφ₂=k₂ получим:

 (9)

12. Условия параллельности и перпендикулярности прямых.

13. Уравнение прямой в отрезках на осях.

14. Общее уравнение прямой на плоскости.

15. Решение неравенств на плоскости.

Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным,необходимо перенести все его члены в одну часть, т.e. привести к виду: f ( x ) > 0 , 

и построить график функции  y = f ( x ). После этого, используя построенный график, можно найти нули функции (см. выше), которые разделят ось  Х  на несколько интервалов. Теперь на основе этого определим интервалы  x, внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции:  a  и  b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых  f ( x ) > 0:  x < a  и  x > b ( они выделены жирными стрелками ). Ясно, что знак  >  здесь условный; вместо него может быть любой другой:  < ,  ,  .

Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т.e. привести неравенства к виду:

и построить графики функций  y = f ( x ),  y = g ( x ) , ... ,  y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т.e. их общую часть.