
- •1.Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве. Косоугольные системы координат.
- •2. Расстояние между двумя точками прямой, плоскости и в пространстве.
- •3. Деление отрезка в заданном отношении.
- •4. Полярная система координат. Сферическая система координат.
- •5. Переход от декартовой к полярной системе координат и обратно.
- •6. Преобразование координат для прямоугольной системы координат методом сдвига и поворота.
- •7. Алгебраическая линия и её порядок. Теорема об инвариантности порядка.
- •16. Окружность. Общее и каноническое уравнения окружности.
- •17. Эллипс. Каноническое уравнение эллипса и его свойства.
- •18. Парабола. Каноническое уравнение параболы и его свойства.
- •19. Гипербола. Каноническое уравнение гиперболы и его свойства.
- •20. Окружность, эллипс, гипербола и парабола как алгебраические линии второго порядка и как сечения конуса.
- •21. Геометрический вектор (длина вектора, нуль-вектор, равенство геометрических векторов, коллинеарность и компланарность). Координатные орты.
- •22. Линейные операции с геометрическими векторами. Координаты геометрического вектора и его запись с помощью знака суммы. Знак суммирования и его свойства.
- •23. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •27. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •28. Общее уравнение прямой на плоскости в представлении геометрических векторов.
- •38. Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».
- •39. Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.
- •40. Свойства определителя. Терема об определителе произведения квадратных матриц.
- •41. Обратная матрица. Теорема существования и единственности обратной матрицы.
- •42. Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
- •43. Транспонирование и его свойства.
- •44. Система линейных уравнений и её решение.
- •45. Метод Гаусса для решений совместной системы линейных уравнений.
- •46. Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
- •47. Теорема о решении однородной системы линейных уравнений.
- •48. Теорема о числе решений совместной системы линейных уравнений.
- •49. Решение квадратной системы линейных уравнений с помощью обратной матрицы.
- •50. Формулы Крамера.
- •51. Линейное (векторное) пространство. Линейное подпространство.
- •52. Пространство Rn и линейные операции в этом пространстве.
- •53. Система векторов. Линейно зависимые и независимые векторы.
- •54. Базис линейного пространства. Примеры.
- •55. Теорема о разложении вектора по базису.
- •56. Линейная оболочка векторов.
- •57. Векторное представление системы линейных уравнений.
- •58. Теорема Кронекера-Капелли.
- •59. Критерий линейной зависимости векторов в пространстве Rn.
- •60. Евклидовое пространство.
- •61. Нормируемое пространство.
- •62. Ортогональное дополнение и его свойства.
- •63. Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
- •64. Линейная функция. Билинейная форма. Квадратичная форма.
- •65. Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.
- •66. Линейная балансовая модель. ( Модель Леонтьева)
- •67. Модель международной торговли.
- •68. Линейные операторы как отображения. Образ и ядро линейного оператора.
- •69. Взаимно однозначные отображения.
- •70. Произведение операторов. Обратный оператор.
- •71. Теорема о представлении оператора в виде матрицы.
- •72. Произведение линейных отображений.
52. Пространство Rn и линейные операции в этом пространстве.


53. Система векторов. Линейно зависимые и независимые векторы.


54. Базис линейного пространства. Примеры.
Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1) система линейно независима.
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов )
Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке. Эти векторы называются базисными.

55. Теорема о разложении вектора по базису.


56. Линейная оболочка векторов.
Линейная оболочка — это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка — это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:
1) Если задана линейная оболочка — ранг набора векторов равен его размерности. С другой стороны в таком случае рангом или размерностью называют минимальное количество линейно независимых векторов в линейном подпространстве.
57. Векторное представление системы линейных уравнений.
Представим осн. матрицу А в виде в-р-столбцов А1 , А2,…, Ап.
Тогда система лин. ур-ний (6.1) записывается в векторном виде:
x1А1+х2А2+…+хnAn=b
А1=(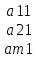 ,
)A2=(
,
)A2=( ,….
An=(
,….
An=(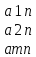 ),b=(
),b=( )
)
Значит, сис. лин. ур-ний тхп мб представлена в виде разложения в-а b€Rm – в-ра свободных членов по n в-рам А1, А2, . . . , А п € R m – в-р-столбцам матрицы коэф., при этом коэф. разложения оказываются переменные.
58. Теорема Кронекера-Капелли.


59. Критерий линейной зависимости векторов в пространстве Rn.
Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.
Доказательство.
Необходимость. Пусть система ![]() линейно
зависимая. Тогда, по определению, она
представляет нулевой вектор нетривиально,
т.е. существует нетривиальная
линейная комбинация
данной системы векторов равная нулевому
вектору:
линейно
зависимая. Тогда, по определению, она
представляет нулевой вектор нетривиально,
т.е. существует нетривиальная
линейная комбинация
данной системы векторов равная нулевому
вектору:
![]() ,
,
где
хотя бы один из коэффициентов этой
линейной комбинации не равен нулю.
Пусть ![]() ,
, ![]() .
.
Разделим
обе части предыдущего равенства на
этот ненулевой коэффициент (т.е. умножим
на ![]() :
:
![]() .
.
Обозначим: ![]() ,
где
,
где ![]() .
.
Тогда
![]()
или ![]()
т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.
Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:
![]() .
.
Перенесем
вектор ![]() в
правую часть этого
равенства:
в
правую часть этого
равенства:
![]() .
.
Так
как коэффициент при векторе ![]() равен
равен ![]() ,
то мы имеем нетривиальное представление
нуля системой векторов
,
то мы имеем нетривиальное представление
нуля системой векторов ![]() ,
что означает, что эта система векторов
является линейно зависимой, ч.т.д.
,
что означает, что эта система векторов
является линейно зависимой, ч.т.д.
Теорема доказана.
Следствие.
1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.
2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.
