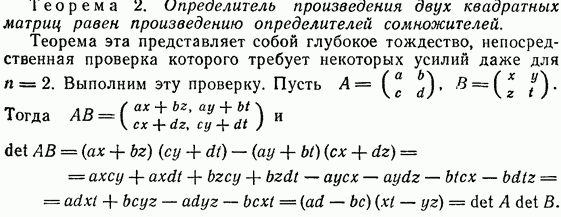
Обратная матрица. Теорема существования и единственности обратной матрицы.

Квадратная матрица А наз. невырожденной, если ее определитель не равен 0.

Всякая невырожденная матрица имеет обратную.

Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.

Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется миноромматрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным. Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.

В матрице  размеров 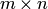 минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.

Рангом матрицы называется порядок базисного минора. В нулевой матрице базисного минора нет. Поэтому ранг нулевой матрицы, по определению полагают равным нулю. Ранг матрицы 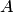 обозначается  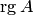. ПримерНайти все базисные миноры и ранг матрицы

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля 

Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.

Транспонирование и его свойства.

Транспонированая матрица получается из исходной путем замены строк столбцами c одинаковыми номерами.

Простая операция, не требующая дополнительных пояснений. Однако для наглядности приведем пример транпонированной матрицы:

Так для матрицы А

Транспонированная матрица будет выглядеть следующим образом.

Полезными будут свойства транспонированных матриц, приведенные ниже.

(А^T)^T=A

(AB)^T=B^TA^T

(A+B)^T=A^T+B^T

detA=detA^T

Система линейных уравнений и её решение.

Различные формы записи системы линейных уравнений.: