Матрица линейного оператора

Пусть 

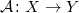
Пусть п.п. 

Пусть п.п. 

, где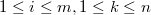 

Линейный оператор 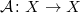 называется автоморфизмом (или гомоморфизмом).

Образ и ядро линейного оператора

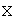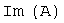Рассмотрим линейный оператор , действующий в конечномерном линейном пространстве . Доказано, что образ линейного оператора  линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается .

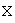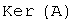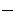Ядром линейного оператора называется множество элементов из , образом которых является нулевой элемент. Ядро оператора обозначают : . Ядро линейного оператора линейное пространство; размерность ядра линейного оператора называется дефектомоператора, обозначается : .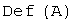

Для линейного оператора, действующего в n-мерном линейном пространстве 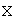, справедливы следующие утверждения:

сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ;

ранг оператора равен рангу его матрицы;

ядро оператора совпадает с множеством  решений линейной однородной системы с матрицей 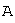, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.

Взаимно однозначные отображения.

Пусть ^A: X_n → X_n — некоторый оператор (не обязательно линейный), D М X_n — область определения и E М X_n — область значений этого оператора.

Оператор ^A:X_n → X_n называется взаимно однозначным, если из равенства образов следует равенство прообразов:

Пусть теперь ^A:X_n → X_n — линейный оператор. Справедлива следующая

Теорема 1. Для того, чтобы линейный оператор ^A:X_n → X_n осуществлял взаимно однозначное отображение, необходимо и достаточно, чтобы Ker ^A = θ .

Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия".

Следствие. Для того, чтобы линейный оператор ^A:X_n → X_n осуществлял взаимно однозначное отображение, необходимо и достаточно, чтобы Rg ^A = n , где n — размерность пространства.

Рассмотрим оператор ^A: X_n → X_n (не обязательно линейный), осуществляющий взаимно однозначное отображение.

Оператор ^B: X_n → X_n называется обратным оператору ^A:D М X_n → X_n , если "x О D :   ^B(^Ax) = x , т.е.

где ^E — тождественный оператор. Обозначая обратный оператор ^A ^{− 1} , получаем определение обратного оператора в виде

Теорема 2. Для того, чтобы оператор ^A: D М X_n → E М X_n имел обратный, необходимо и достаточно, чтобы он осуществлял взаимно однозначное отображение.

Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия".

Произведение операторов. Обратный оператор.

Произведением линейных операторов А и В из 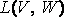 называется оператор АВ, определяемый следующим образом: (А В)А(В для любого  из V. Произведение линейных операторов тоже будет линейным оператором.

Справедливы следующие свойства умножения линейных операторов:

1. АВ) = (А )В.

2. (АВ)Е = А (ВЕ).

3. (А + В)Е = АЕ + ВЕ,  Е(А + В) = ЕА + ЕВ.

Умножение линейных операторов, вообще говоря, некоммутативно.

Легко увидеть, что для всякого линейного оператора А  А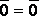. При этом если А только при , то оператор называется невырожденным; если же найдется такой вектор , что А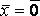, то оператор А– вырожденный.

Линейный оператор В  из  называется обратным для оператора А из , если выполняется соотношение АВ = ВА = Е. Обратный оператор обычно обозначается как А^–1. Для того чтобы линейный оператор А из  имел обратный, необходимо и достаточно, чтобы он был невырожденным.

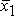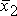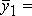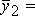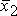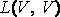Будем говорить, что линейный оператор А действует взаимно однозначно из V в V, если любым двум различным элементам  и  отвечают различные элементы А и А. Для того чтобы линейный оператор А  из  имел обратный, необходимо и достаточно, чтобы этот оператор действовал взаимно однозначно из V в V.

Теорема о представлении оператора в виде матрицы.

Произведение линейных отображений.