Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.

Решение квадратной системы линейных уравнений с помощью обратной матрицы.

Пусть имеется квадратная матрица n-го порядка

Матрица А^-1 называется обратной матрицей по отношению к матрице А, если А*А^-1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

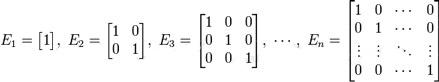
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.

Теорема условия существования обратной матрицы

Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.

Матрица А = (А1, А2,...А_n) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.

Алгоритм нахождения обратной матрицы

Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.

Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.

Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.

Записать обратную матрицу А^-1, которая находится в последней таблице под матрицей Е исходной таблицы.

Формулы Крамера.

Если в системе  линейных уравнений с  неизвестными  , то система имеет решение и притом единственное. Это решение задается формулами

Доказательство. Обратная матрица находится по формуле

где  -- алгебраические дополнения. Тогда

Заметим, что разложение определителя  по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя  по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому

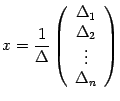  , откуда и следует утверждение теоремы.  

Линейное (векторное) пространство. Линейное подпространство.

Про-во наз. Лин. Пр-вом, если для любых эл-в х, у, z того про-ва и произвол. веществ.чисел µ, v выполняются след. св-ва:

А1. х + у = у + х

А2. х + {у + z) = (х + у) + z.

АЗ. Особ. роль веществ.единицы: 1*х= х.

А4 - µ(v х) = v (µ х).

А5. Сущ. нул. эл-т., к-рый обозначается символом О, что х +0 = х.

А 6 . Для всякого элемента х сущ-т противоп.эл- т ẍ этого про-ва такой, что: х+ẍ=О.

А7. (µ+v)x = µх+ vх

А 8 . µ (x + у) = µх+µу

Эл-ты лин. про-ва наз. векторами. Само лин. про-во будем обозначать L. примеры лин.пр-ва

1.геом.вектора;

2.матрица,

3.ф-ции,

4.n-мерный в-р –упоряд.набор п-чисел,для к-рых справедливы