
- •Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве
- •Расстояние между двумя точками прямой, плоскости и в пространстве.
- •Деление отрезка в заданном отношении. Понятие деления отрезка в данном отношении
- •Формулы деления отрезка в данном отношении на плоскости
- •Формулы координат середины отрезка
- •Полярная система координат. Сферическая система координат.
- •Переход от декартовой к полярной системе координат и обратно.
- •Преобразование координат для прямоугольной системы координат методом сдвига и поворота.
- •Окружность. Общее и каноническое уравнения окружности.
- •Эллипс. Каноническое уравнение эллипса и его свойства.
- •Линейные операции с геометрическими векторами. Координаты геометрического вектора и его запись с помощью знака суммы. Знак суммирования и его свойства.
- •Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •Действия с геометрическими векторами в координатной форме.
- •Признак коллинеарности векторов.
- •Скалярное произведение геометрических векторов и его свойства.
- •Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •Общее уравнение прямой на плоскости в представлении геометрических векторов.
- •Каноническое и параметрическое уравнения прямой в пространстве.
- •Общее уравнение плоскости в пространстве.
- •Решение неравенств на плоскости.
- •Расстояние от точки до плоскости.
- •Векторное произведение векторов и его свойства.
- •Формулы вычисления векторного произведения векторов
- •Свойства векторного произведения векторов
- •Запись векторного произведения векторов с помощью определителя.
- •Смешанное произведение векторов.
- •Решение систем линейных уравнений с помощью векторного произведения.
- •Матрицы и их классификация. Действия с матрицами. Экономические примеры.
- •Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».
- •Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.
- •Свойства определителя. Терема об определителе произведения квадратных матриц.
- •Обратная матрица. Теорема существования и единственности обратной матрицы.
- •Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
- •Транспонирование и его свойства.
- •Система линейных уравнений и её решение.
- •Метод Гаусса для решений совместной системы линейных уравнений.
- •Прямой ход.
- •Обратный ход.
- •Замечания:
- •Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
- •Теорема о решении однородной системы линейных уравнений.
- •Теорема о числе решений совместной системы линейных уравнений.??????????
- •Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
- •Решение квадратной системы линейных уравнений с помощью обратной матрицы.
- •Теорема условия существования обратной матрицы
- •Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
- •Алгоритм нахождения обратной матрицы
- •Формулы Крамера.
- •Линейное (векторное) пространство. Линейное подпространство.
- •Единтс-ный ему противопол.
- •Лин.Подпр-во.
- •Базис линейного пространства. Примеры.
- •Теорема о разложении вектора по базису.
- •Линейная оболочка векторов.
- •Векторное представление системы линейных уравнений.
- •Теорема Кронекера-Капелли.
- •Критерий линейной зависимости векторов в пространстве Rn.
- •Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
- •Евклидовое пространство.
- •Нормируемое пространство.
- •Ортогональное дополнение и его свойства.
- •Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
- •Линейная функция. Билинейная форма. Квадратичная форма.
- •Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.
- •Линейная балансовая модель.
- •Модель международной торговли.
- •Линейные операторы как отображения. Образ и ядро линейного оператора.
- •Матрица линейного оператора
- •Образ и ядро линейного оператора
- •Взаимно однозначные отображения.
- •Произведение операторов. Обратный оператор.
- •Теорема о представлении оператора в виде матрицы.
- •Произведение линейных отображений.
-
Геометрический вектор (длина вектора, нуль-вектор, равенство геометрических векторов, коллинеарность и компланарность). Координатные орты.
-
Вектор- называется всякая величина, обладающая направлением. Вектор, началом которого служит точка А, а концом точка- В, обозначается АВ.
-
Длина вектора, также называется модулем. Модуль это скалярная величина, обозначается двумя вертикальными чертами.
-
Нуль-вектор- это вектор длина которого равна 0.
-
Равенство векторов- два(ненулевых)вектора а и b равны, если они равнонаправленные и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны. Вектор можно переносить параллельно самому себе , а начало вектора помещать в любую точку О пространства. Равные векторы так же называют свободными.
-
Коллинеарные – векторы а иb называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают, а||b. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.
-
Компланарные- три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов, хотя бы один нулевой или два любые коллинеарные, то такие векторы компланарны.
-
Орт вектор- вектор, длина которого равна единице, называется единичным вектором и обозначается через ē. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора а и обозначается а°.
-
-
Линейные операции с геометрическими векторами. Координаты геометрического вектора и его запись с помощью знака суммы. Знак суммирования и его свойства.
-
Произведением вектора
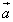 на
число
на
число 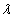 называется
вектор, получающийся из вектора
называется
вектор, получающийся из вектора 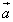 растяжением
(при
растяжением
(при 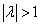 )
или сжатием (при
)
или сжатием (при 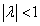 )
в
)
в 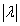 раз,
причём направление вектора
раз,
причём направление вектора 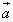 сохраняется,
если
сохраняется,
если 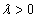 ,
и меняется на противоположное, если
,
и меняется на противоположное, если 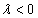 .
(Рис. 2)
.
(Рис. 2) -
Из определения следует, что векторы
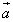 и
и 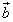 =
= 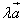 всегда
расположены на одной или на параллельных
прямых. Такие векторы называютсяколлинеарными.
(Можно говорить также, что эти векторы
параллельны, однако в векторной алгебре
принято говорить "коллинеарны".)
Справедливо и обратное утверждение:
если векторы
всегда
расположены на одной или на параллельных
прямых. Такие векторы называютсяколлинеарными.
(Можно говорить также, что эти векторы
параллельны, однако в векторной алгебре
принято говорить "коллинеарны".)
Справедливо и обратное утверждение:
если векторы 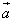 и
и 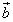 коллинеарны,
то они связаны отношением
коллинеарны,
то они связаны отношением -
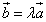 .
(1)
.
(1)
-
Следовательно, равенство (1) выражает условие коллинеарности двух векторов.
-
Суммой векторов
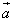 и
и 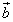 называется
вектор
называется
вектор 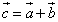 ,
начало которого совпадает с началом
вектора
,
начало которого совпадает с началом
вектора 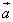 ,
а конец - с концом вектора
,
а конец - с концом вектора 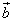 ,
при условии, что начало вектора
,
при условии, что начало вектора 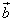 приложено
к концу вектора
приложено
к концу вектора 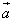 .
(Рис. 3)
.
(Рис. 3) 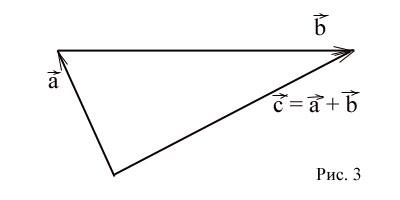
-
Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n свободных векторов
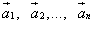 .
Если к концу вектора
.
Если к концу вектора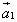 приложить
начало вектора
приложить
начало вектора 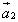 ,
а к концу вектора
,
а к концу вектора 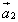 -
начало вектора
-
начало вектора  и
т.д. и, наконец, к концу вектора
и
т.д. и, наконец, к концу вектора 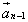 -
начало вектора
-
начало вектора 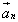 ,
то суммой этих векторов служит замыкающий
вектор
,
то суммой этих векторов служит замыкающий
вектор 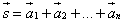 ,
начало которого совпадает с началом
первого вектора
,
начало которого совпадает с началом
первого вектора 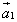 ,
а конец - с концом последнего вектора
,
а конец - с концом последнего вектора 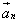 .
(Рис. 4)
Слагаемые
.
(Рис. 4)
Слагаемые 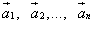 называются
составляющими вектора
называются
составляющими вектора 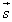 ,
а сформулированное правило - правилом
многоугольника.
Этот многоугольник может и не быть
плоским.
,
а сформулированное правило - правилом
многоугольника.
Этот многоугольник может и не быть
плоским.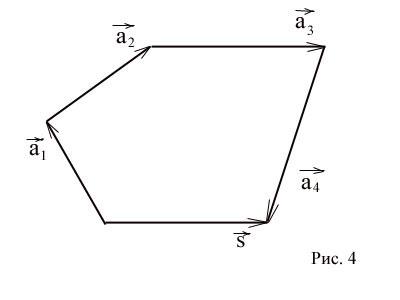
-
При умножении вектора
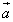 на
число -1 получается противоположный
вектор
на
число -1 получается противоположный
вектор 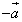 .
Векторы
.
Векторы 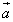 и
и 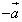 имеют
одинаковые длины и противоположные
направления. Их сумма
имеют
одинаковые длины и противоположные
направления. Их сумма 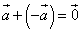 даёт нулевой
вектор,
длина которого равна нулю. Направление
нулевого вектора не определено.
даёт нулевой
вектор,
длина которого равна нулю. Направление
нулевого вектора не определено. -
В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора
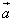 вектор
вектор 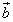 означает
прибавить к вектору
означает
прибавить к вектору 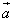 противоположный
вектор
противоположный
вектор 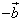 ,
т.е.
,
т.е. 

-
Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
-
Выделим на корд.осях единичные векторы: I,j,k. Выберем произв.вектор а пространства и совместим его начало с началом коорд: а=ОМ. Найдем проекции вектора а на коорд оси. Проведем через конец вектора ОМ плоскочти, параллельные координатным плоскостям. Точки пересеч этих плоскостей с осями обозначим через М1,М2,М3. Получим прямоуг парал-пед,одной из диагоналей которого является вектор ОМ. По опред суммы векторв находим: а=ОМ1+M1N+NM. А так как M1N=OM2, NM=OM3,то а=ОМ1+ОМ2+ОМ3. ОМ1=|ОМ1|i и тд. Обозначим проекции вектора на оси|ОМ1|=аy итд. В итоге получается: a=ax на i+ay на j+ az на k.
-
-
-
-
-
Действия с геометрическими векторами в координатной форме.
-
Пусть даны два вектора
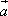 и
и 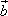 ,
заданные своими проекциями:
,
заданные своими проекциями: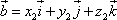
-
или

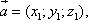
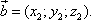
-
или
-
Укажем действия над этими векторами.
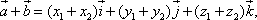
-
1.Сложение:
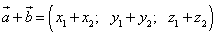
-
или, что то же
-
т.е. при сложении двух векторов одноимённые координаты складываются.
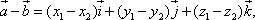
-
2.Вычитание:
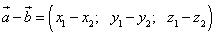
-
или, что то же,
-
т.е. при вычитании двух векторов одноимённые координаты вычитаются.
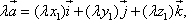
-
3.Умножение вектора на число:
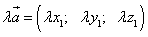
-
или, что то же
-
т.е. при умножении вектора на число все координаты умножаются на это число
-
-
-
Признак коллинеарности векторов.
-
Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением
-
.Пусть даны векторы
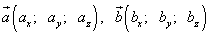 .
Эти векторы коллинеарны, если координаты
векторов связаны отношением
.
Эти векторы коллинеарны, если координаты
векторов связаны отношением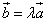
-
,
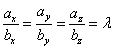
-
то есть, координаты векторов пропорциональны.
-
Скалярное произведение геометрических векторов и его свойства.
-
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
-
a · b = |a| · |b| cos α
-
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a иb.
-
-
Формулы скалярного произведения векторов заданных координатами
-
Формула скалярного произведения векторов для плоских задач
-
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
-
a · b = ax · bx + ay · by
-
-
Формула скалярного произведения векторов для пространственных задач
-
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
-
a · b = ax · bx + ay · by + az · bz
-
-
Формула скалярного произведения n -мерных векторов
-
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; ... ; an} и b = {b1 ; b2 ; ... ; bn} можно найти воспользовавшись следующей формулой:
-
a · b = a1 · b1 + a2 · b2 + ... + an · bn
-
-
Свойства скалярного произведения векторов
-
Скалярное произведение вектора самого на себя всегда больше или равно нуля:
-
a · a ≥ 0
-
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
-
a · a = 0 <=> a = 0
-
Скалярное произведение вектора самого на себя равно квадрату его модуля:
-
a · a = |a|2
-
Операция скалярного умножения коммуникативна:
-
a · b = b · a
-
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
-
a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b
-
(αa) · b = α(a · b)
-
Операция скалярного умножения дистрибутивна:
