(a + b) · c = a · c + b · c

Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.

Скалярное произведение векторов равно сумме произведений их одноименных координат.

Дов-во: а=ах на i+ ay на j+ az на k b=bx на i+by на j+ bz на k

Найдем скалярное произведение перемножая как многочлены. По таблице скалярного произведения векторов: i на i=1, i на j=0, I на k=0 и тд. В итоге у нас останется: аb=axbx+ayby+azbz

Длина вектора: это длина отрезка и обозначается как |AB|. Вектор длина которого равна 1 – единичный вектор. Обознач как е. Если рассматривать АВ,где A(x1) и B(x2) точки на корд прямой,то расстояние АВ=|х2-х1|

Расстояние между двумя точками: на плоскости: АВ= (y1-y2)²+(x1-x2)² все под корнем. Пусть в системе корд заданы две точки А(х1,у1) и В(х2,у2). Из этих точек опусти перпендикуляры на ось Ох,из точки В на Оу. |АВ|=АМ²+ВМ² все под корнем. В пространстве: тоже самое плюс z.

Косинус угла между векторами: cos α=AB на AC\ |AB| на |AC| или ab\ |a| |b|.

Общее уравнение прямой на плоскости в представлении геометрических векторов.

Покажем, что Ах+ Ву+С=о есть уравнение прямой линии. Возможны два случая:

Если В=0,то ур-ние имеет вид Ах+С=0, причем А не равно 0,т.е х=-с/а. Это есть ур-ние прямой, ||оси Оу и проходящей через точку (-с/а; 0)

Если В не равно 0,то из ур-ния получаем у=-А/в*х-с/в. Это есть ур-ние прямой с угловым коэф. K=tg(альфа)=-а/в. Итак, ур-ние есть ур-ние прямой линии, оно называется общим уравнением прямой.

Некоторые частные случаи общего ур-ния прямой :

1)если А=0,то ур-ние приводится к виду у=-с/в.Это есть ур-ние прямой,параллельной оси Ох.

2)Если В=0,то прямая || оси Оу

.

3)Если С=0,то получаем Ах+Ву=0. Уравнению удовлетворяют координаты точки О(0;0), прямая проходит через начало координат.

Каноническое и параметрическое уравнения прямой в пространстве.

Параметрическое уравнение прямой: х=x0+mt, y=y0+nt, z=z0+pt все в системе. Векторное уравнение прямой,записанное в другом виде. Учитывая,что r=(x,y,z), r0=(x0,y0,z0), tS=(tm,tn,tp).

Каноническое уравнение прямой: x-x0\ m = y-y0\ n = z-z0\p. Уравнение можно было бы получить сразу из параметрического,исключив параметр t.

Общее уравнение плоскости в пространстве.

Ax+By+Cz+D=0-общее уравнение плоскости. Уравнение определяет в системе координат некоторую плоскость

Частные случаи.

Если D=0,то плоскость проходит через начало координат. Ax+By+Cz=0, этому ур-ию удовлетворяет точка О(о,о,о)

Если С=0,то плоскость параллельна оси Oz. Ax+By+D=0

Если В=0,то параллельна оси Оу

Если А=0,то параллельна оси Ох

Если С=D=0,то плоскость проходит через О(0,0,0) параллельно Оz,т.е плоскость проходит через Oz. Аналогично,A=D проходит через Ох и В=D проходит через Оу.

Если А=В=0,то плоскость параллельна Оху. Аналогично, B=C параллельна Oyz и A=C параллельна Oxz.

Если A=B=D=0, то это уравнение плоскости Оху. Аналогично, у=0-уравнение Охz, х=0-уравнение Оуz

Решение неравенств на плоскости.

Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным,необходимо перенести все его члены в одну часть, т.e. привести к виду: f ( x ) > 0 , 

и построить график функции  y = f ( x ). После этого, используя построенный график, можно найти нули функции (см. выше), которые разделят ось  Х  на несколько интервалов. Теперь на основе этого определим интервалы  x, внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции:  a  и  b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых  f ( x ) > 0:  x < a  и  x > b ( они выделены жирными стрелками ). Ясно, что знак  >  здесь условный; вместо него может быть любой другой:  < ,  ,  .

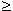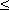Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т.e. привести неравенства к виду:

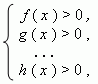
и построить графики функций  y = f ( x ),  y = g ( x ) , ... ,  y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т.e. их общую часть.

Расстояние от точки до плоскости.

Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость. Формула для вычисления расстояния от точки до плоскости

Векторное произведение векторов и его свойства.

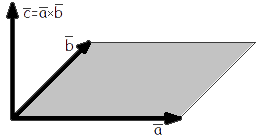
Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах aи b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:

a × b = {a_yb_z - a_zb_y; a_zb_x - a_xb_z; a_xb_y - a_yb_x}

Свойства векторного произведения векторов

 Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:

S_парал = [a × b]

 Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:

Запись векторного произведения векторов с помощью определителя.

Смешанное произведение векторов.

Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Формулы вычисления смешанного произведения векторов

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {a_x; a_y; a_z}, b = {b_x; b_y; b_z} и c = {c_x; c_y; c_z} в декартовой системе координат можно вычислить, используя следующую формулу:

Свойства смешанного произведения векторов

 Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:

V_парал = |a · [b × c]|

 Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов: