Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».

Определителем матрицы называется некоторая математическая функция элементов квадратной матрицы, результатом которой является число. Обозначение: 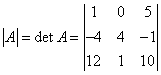 — определитель 3- го порядка (т.к. матрица размера 3 на 3) матрицы А. Замечание: В этом, якобы простом, определении определителя ( звучит как тавтология) говориться, что с элементами матрицы нужно что то сделать ( умножить, сложить, разделить и т.д.) и получится значение определителя этой матрицы. Однако не сказано. Что же все-таки надо с ними сделать.

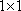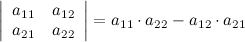Вычисление определителей первого порядка. Матрица размера  это просто число. Определителем такой матрицы является само это число. Вычисление определителей второго порядка. Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:   Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.

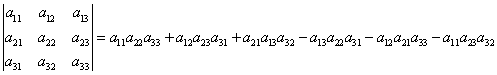Вычисление определителей третьего порядка. Определитель третьего порядка вычисляется по правилу: Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:   Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":

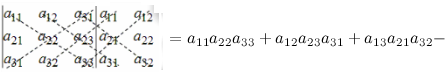
Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.

Определителем второго порядка, соответствующим таблице элементов

называется число a₁ b₂ - a₂ b₁. Определитель второго порядка обозначается так:

Таким образом, 

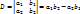
Определитель третьего порядка, соответствующий таблице элементов 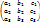 определяется равенством

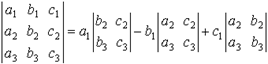
Минором данного элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент. Алгебраическим дополнением данного элемента называется его минор, умноженный на ( - 1)^k, где k - сумма номеров строки и столбца, содержащих данный элемент. A_ij = (-1)^i + j · M_ij Таким образом, знак, который при этом приписывается минору соответствующего элемента определителя, определяется следующей таблицей: 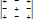  В приведенном выше равенстве, выражающем определитель третьего порядка, в правой части стоит сумма произведений элементов первой строки определителя на их алгебраические дополнения.

Свойства определителя. Терема об определителе произведения квадратных матриц.

Квадратной матрице 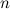 -го порядка ставиться в соответствие число, называемоеопределителем матрицы или детерминантом.

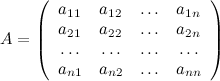
При транспонировании квадратной матрицы её определитель не меняется:

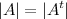
Общий множитель в строке можно выносить за знак определителя.

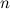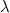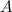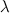То есть, если квадратная матрица  -го порядка умножается на некоторое ненулевое число , то определитель полученной матрицы равен произведению определителя исходной матрицы  на число  в степени, равной порядку матриц.

Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

Если две строки определителя поменять местами, то определитель поменяет знак.

Определитель с двумя равными строками равен нулю.

Определитель с двумя пропорциональными строками равен нулю.