
- •Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве
- •Расстояние между двумя точками прямой, плоскости и в пространстве.
- •Деление отрезка в заданном отношении. Понятие деления отрезка в данном отношении
- •Формулы деления отрезка в данном отношении на плоскости
- •Формулы координат середины отрезка
- •Полярная система координат. Сферическая система координат.
- •Переход от декартовой к полярной системе координат и обратно.
- •Преобразование координат для прямоугольной системы координат методом сдвига и поворота.
- •Окружность. Общее и каноническое уравнения окружности.
- •Эллипс. Каноническое уравнение эллипса и его свойства.
- •Линейные операции с геометрическими векторами. Координаты геометрического вектора и его запись с помощью знака суммы. Знак суммирования и его свойства.
- •Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •Действия с геометрическими векторами в координатной форме.
- •Признак коллинеарности векторов.
- •Скалярное произведение геометрических векторов и его свойства.
- •Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •Общее уравнение прямой на плоскости в представлении геометрических векторов.
- •Каноническое и параметрическое уравнения прямой в пространстве.
- •Общее уравнение плоскости в пространстве.
- •Решение неравенств на плоскости.
- •Расстояние от точки до плоскости.
- •Векторное произведение векторов и его свойства.
- •Формулы вычисления векторного произведения векторов
- •Свойства векторного произведения векторов
- •Запись векторного произведения векторов с помощью определителя.
- •Смешанное произведение векторов.
- •Решение систем линейных уравнений с помощью векторного произведения.
- •Матрицы и их классификация. Действия с матрицами. Экономические примеры.
- •Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».
- •Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.
- •Свойства определителя. Терема об определителе произведения квадратных матриц.
- •Обратная матрица. Теорема существования и единственности обратной матрицы.
- •Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
- •Транспонирование и его свойства.
- •Система линейных уравнений и её решение.
- •Метод Гаусса для решений совместной системы линейных уравнений.
- •Прямой ход.
- •Обратный ход.
- •Замечания:
- •Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
- •Теорема о решении однородной системы линейных уравнений.
- •Теорема о числе решений совместной системы линейных уравнений.??????????
- •Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
- •Решение квадратной системы линейных уравнений с помощью обратной матрицы.
- •Теорема условия существования обратной матрицы
- •Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
- •Алгоритм нахождения обратной матрицы
- •Формулы Крамера.
- •Линейное (векторное) пространство. Линейное подпространство.
- •Единтс-ный ему противопол.
- •Лин.Подпр-во.
- •Базис линейного пространства. Примеры.
- •Теорема о разложении вектора по базису.
- •Линейная оболочка векторов.
- •Векторное представление системы линейных уравнений.
- •Теорема Кронекера-Капелли.
- •Критерий линейной зависимости векторов в пространстве Rn.
- •Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
- •Евклидовое пространство.
- •Нормируемое пространство.
- •Ортогональное дополнение и его свойства.
- •Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
- •Линейная функция. Билинейная форма. Квадратичная форма.
- •Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.
- •Линейная балансовая модель.
- •Модель международной торговли.
- •Линейные операторы как отображения. Образ и ядро линейного оператора.
- •Матрица линейного оператора
- •Образ и ядро линейного оператора
- •Взаимно однозначные отображения.
- •Произведение операторов. Обратный оператор.
- •Теорема о представлении оператора в виде матрицы.
- •Произведение линейных отображений.
-
-
Решение систем линейных уравнений с помощью векторного произведения.
-
Множество точек плоскости, координаты которых удовлетворяют неравенству Ax+By+C>0 илиAx+By+C<0, образуют область или множество решений соответствующего неравенства.
-
Теорема (5). Область решений неравенства Ax+By+C≤0 является полуплоскостью, ограниченная прямой Ax+By+C=0.
-
Доказательство. Известно, что вектор
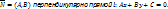 В
каждой из полуплоскостей, ограниченных
прямой Ax+By+C=0, отметим по точке:
В
каждой из полуплоскостей, ограниченных
прямой Ax+By+C=0, отметим по точке: 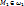 и
и 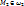 .
. -
На прямой l отметим точку
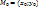 ,
для координат которых:
,
для координат которых: -
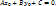
-
 Из
рисунка видно, что скалярные произведения
векторов
Из
рисунка видно, что скалярные произведения
векторов 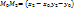 ,
, 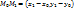 и
вектора N, дает неравенства:
и
вектора N, дает неравенства: -
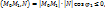
-
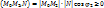
-
(т.к.
 –
острый и cos
–
острый и cos  >0,
>0,  –
тупой угол и cos
–
тупой угол и cos  <0)
или например, для вектора
<0)
или например, для вектора  ,
считая, что точка М – эта любая точка
полуплоскости
,
считая, что точка М – эта любая точка
полуплоскости  ,
включая точки прямой l будет
выполняться неравенство:
,
включая точки прямой l будет
выполняться неравенство: -
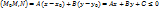
-
Матрицы и их классификация. Действия с матрицами. Экономические примеры.
-
-
экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики набор стратегически значимых переменных; указывают направление движения ресурсов.
-
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля(например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк истолбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задает размер матрицы.
-
Классификация:
-
Матрица, у которой все элементы выше (ниже) главной диагонали равны нулю, называются нижне- (верхнетреугольной) или просто треугольной;
-
Матрица, у которой равное число строк и столбцов называют квадратной. Квадратная матрица размера
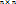 называется
квадратной матрицей порядка n;
называется
квадратной матрицей порядка n; -
Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной;
-
Диагональная матрица, у которой все элементы главной диагонали равны между собой, называется скалярной;
-
Скалярная матрица, у которой все элементы главной диагонали равны 1, называют единичной матрицей и обозначают как Е;
-
Матрица
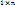 называется
вектор-строкой длины n, а матрица
называется
вектор-строкой длины n, а матрица 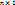 –
вектор-столбцом длины n.
–
вектор-столбцом длины n.
-
Если у матрицы поменять местами строки и столбцы, то такая матрица называется транспонированной.
-
Элементы матрицы, имеющие одинаковые индексы, образуют главную диагональ матрицы.
-
В отличии от умножения деление матрицы не определено, его заменяют умножением на обратную матрицу. Матрицу В называют обратной матрице А, если А*В=В*А=Е. Обратная матрица существует только у квадратной матрицы и то не всегда. Если обратной не существует, то про такую матрицу говорят что она вырождена или особенная.
-
Действия с матрицами:
-
Сложение (операция сложения вводится только для матриц одинаковых размеров);
-
Умножение на число;
-
Элементарные преобразования матриц:
-
Перестановка местами двух параллельных рядов;
-
Умножение всех элементов ряда матрицы на число, отличное от 0;
-
Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
-
-
Произведение матриц (операция умножения двух матриц вводится только для случая, когда число столбоцов первой матрицы равно числу строк второй матрицы).
