
- •Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве
- •Расстояние между двумя точками прямой, плоскости и в пространстве.
- •Деление отрезка в заданном отношении. Понятие деления отрезка в данном отношении
- •Формулы деления отрезка в данном отношении на плоскости
- •Формулы координат середины отрезка
- •Полярная система координат. Сферическая система координат.
- •Переход от декартовой к полярной системе координат и обратно.
- •Преобразование координат для прямоугольной системы координат методом сдвига и поворота.
- •Окружность. Общее и каноническое уравнения окружности.
- •Эллипс. Каноническое уравнение эллипса и его свойства.
- •Линейные операции с геометрическими векторами. Координаты геометрического вектора и его запись с помощью знака суммы. Знак суммирования и его свойства.
- •Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •Действия с геометрическими векторами в координатной форме.
- •Признак коллинеарности векторов.
- •Скалярное произведение геометрических векторов и его свойства.
- •Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.
- •Общее уравнение прямой на плоскости в представлении геометрических векторов.
- •Каноническое и параметрическое уравнения прямой в пространстве.
- •Общее уравнение плоскости в пространстве.
- •Решение неравенств на плоскости.
- •Расстояние от точки до плоскости.
- •Векторное произведение векторов и его свойства.
- •Формулы вычисления векторного произведения векторов
- •Свойства векторного произведения векторов
- •Запись векторного произведения векторов с помощью определителя.
- •Смешанное произведение векторов.
- •Решение систем линейных уравнений с помощью векторного произведения.
- •Матрицы и их классификация. Действия с матрицами. Экономические примеры.
- •Определитель 1-го, 2-го и третьего порядков. Правило Саррюса и «звёздочки».
- •Минор и алгебраическое дополнение элемента определителя. Определитель произвольного порядка.
- •Свойства определителя. Терема об определителе произведения квадратных матриц.
- •Обратная матрица. Теорема существования и единственности обратной матрицы.
- •Минор матрицы. Базисный минор. Ранг матрицы. Нахождение ранга матрицы с помощью элементарных преобразований.
- •Транспонирование и его свойства.
- •Система линейных уравнений и её решение.
- •Метод Гаусса для решений совместной системы линейных уравнений.
- •Прямой ход.
- •Обратный ход.
- •Замечания:
- •Однородная, неоднородная, совместная, несовместная, определенная и неопределенная система. Матричная запись системы линейных уравнений.
- •Теорема о решении однородной системы линейных уравнений.
- •Теорема о числе решений совместной системы линейных уравнений.??????????
- •Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
- •Решение квадратной системы линейных уравнений с помощью обратной матрицы.
- •Теорема условия существования обратной матрицы
- •Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
- •Алгоритм нахождения обратной матрицы
- •Формулы Крамера.
- •Линейное (векторное) пространство. Линейное подпространство.
- •Единтс-ный ему противопол.
- •Лин.Подпр-во.
- •Базис линейного пространства. Примеры.
- •Теорема о разложении вектора по базису.
- •Линейная оболочка векторов.
- •Векторное представление системы линейных уравнений.
- •Теорема Кронекера-Капелли.
- •Критерий линейной зависимости векторов в пространстве Rn.
- •Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
- •Евклидовое пространство.
- •Нормируемое пространство.
- •Ортогональное дополнение и его свойства.
- •Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
- •Линейная функция. Билинейная форма. Квадратичная форма.
- •Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы.
- •Линейная балансовая модель.
- •Модель международной торговли.
- •Линейные операторы как отображения. Образ и ядро линейного оператора.
- •Матрица линейного оператора
- •Образ и ядро линейного оператора
- •Взаимно однозначные отображения.
- •Произведение операторов. Обратный оператор.
- •Теорема о представлении оператора в виде матрицы.
- •Произведение линейных отображений.
-
] S л.н.з.Но ее посис.S’ л.з. по утр.2 вся сис. л.з. Что противор.усл.-->предположение неверно.
-
4.Каждая подсис.л.н.з.сис.в-ров сама л.н.
-
] S={а1,…,аn} ;SэS’={аi1,…aik},i*k=n
-
Т.к.S’- л.з.подсис. --> сущ.нетривиальный набор чисел α1…αn,такой что α1*
-
-
Макс.число л.н.з.в-ров сис. наз.рангом этой системы.
-
-
-
Базис линейного пространства. Примеры.
-
-
Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
-
1) система линейно независима.
-
2) Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов )
-
Базис в пространстве R в степени n (канонический базис). Примеры: Базисом в пространстве называются три некомпланарных вектора , взятые в определённом порядке. Эти векторы называются базисными.
-
-
Теорема о разложении вектора по базису.
-
Определение. Пусть
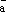 –
произвольный вектор,
–
произвольный вектор,  –
произвольная система векторов.
Если выполняется равенство
–
произвольная система векторов.
Если выполняется равенство -
, (1)
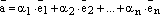
-
то говорят, что вектор
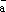 представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов
представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов 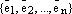 является
базисом векторного пространства,
то равенство (1)
называется разложением вектора
является
базисом векторного пространства,
то равенство (1)
называется разложением вектора 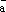 по
базису
по
базису 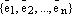 . Коэффициенты
линейной комбинации
. Коэффициенты
линейной комбинации 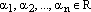 называются
в этом случае координатами
вектора
называются
в этом случае координатами
вектора 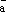 относительно
базиса
относительно
базиса 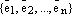 .
. -
Теорема. (О разложении вектора по базису.)
-
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
-
Доказательство. 1) Пусть L произвольная прямая (или ось) и
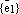 –базис
–базис 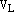 .
Возьмем произвольный вектор
.
Возьмем произвольный вектор 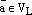 .
Так как оба вектора
.
Так как оба вектора 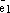 и
и 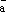 коллинеарные
одной и той же прямой L,
то
коллинеарные
одной и той же прямой L,
то 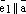 .
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как
.
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как 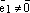 ,
то найдется (существует) такое число
,
то найдется (существует) такое число 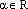 ,
что
,
что 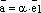 и
тем самым мы получили разложение
вектора
и
тем самым мы получили разложение
вектора 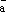 по
базису
по
базису 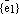 векторного пространства
векторного пространства 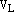 .
. -
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора
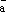 по
базису
по
базису 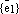 векторного пространства
векторного пространства 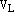 :
: -
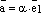 и
и 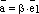 ,
где
,
где 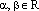 .
Тогда
.
Тогда 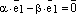 и
используя закон дистрибутивности,
получаем:
и
используя закон дистрибутивности,
получаем: -
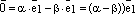 .
. -
Так как
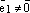 ,
то из последнего равенства следует,
что
,
то из последнего равенства следует,
что 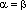 ,
ч.т.д.
,
ч.т.д. -
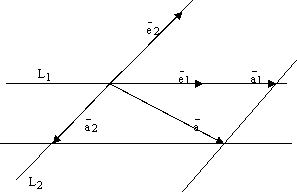
2) Пусть теперь Р произвольная плоскость и
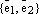 – базис
– базис 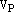 .
Пусть
.
Пусть 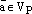 произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую
произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую 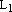 ,
на которой лежит вектор
,
на которой лежит вектор 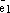 , прямую
, прямую  ,
на которой лежит вектор
,
на которой лежит вектор  .
Через конец вектора
.
Через конец вектора  проведем прямую параллельную
вектору
проведем прямую параллельную
вектору  и
прямую параллельную вектору
и
прямую параллельную вектору 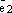 .
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма
.
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма 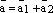 ,
и
,
и 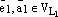 ,
, 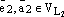 ,
, 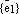 – базис
– базис 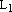 ,
, 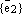 – базис
– базис 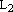 .
.
-
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа
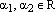 ,
что
,
что -
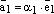 и
и 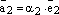 .
Отсюда получаем:
.
Отсюда получаем: -
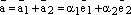 и
возможность разложения по базису
доказана.
и
возможность разложения по базису
доказана. -
-
рис.3.
-
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора
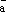 по
базису
по
базису 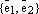 векторного пространства
векторного пространства 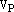 :
: 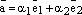 и
и 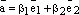 .
Получаем равенство
.
Получаем равенство -
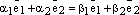 ,
откуда следует
,
откуда следует 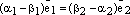 .
Если
.
Если 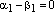 ,
то
,
то 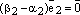 ,
а т.к.
,
а т.к. 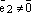 ,
то
,
то 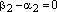 и
коэффициенты разложения равны:
и
коэффициенты разложения равны: 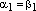 ,
, 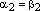 .
Пусть теперь
.
Пусть теперь 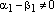 .
Тогда
.
Тогда 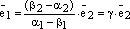 ,
где
,
где 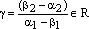 .
По теореме о коллинеарности двух векторов отсюда
следует, что
.
По теореме о коллинеарности двух векторов отсюда
следует, что 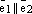 .
Получили противоречие условию теоремы.
Следовательно,
.
Получили противоречие условию теоремы.
Следовательно, 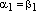 и
и 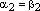 ,
ч.т.д.
,
ч.т.д. -
3) Пусть
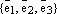 – базис
– базис 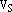 и
пусть
и
пусть 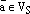 произвольный
вектор. Проведем следующие построения.
произвольный
вектор. Проведем следующие построения. -
Отложим все три базисных вектора
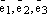 и
вектор
и
вектор 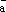 от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы 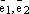 , плоскость
, плоскость 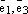 и плоскость
и плоскость 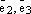 ;
далее через конец вектора
;
далее через конец вектора  проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед:
проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед: -
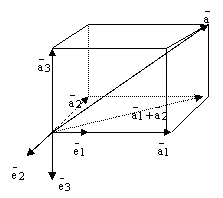
-
рис.4.
-
По правилу сложения векторов получаем равенство:
-
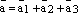 .
(1)
.
(1) -
По построению
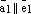 .
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число
.
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число 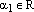 ,
такое что
,
такое что 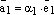 .
Аналогично,
.
Аналогично, 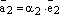 и
и 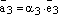 ,
где
,
где 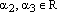 .
Теперь, подставляя эти равенства в (1),
получаем:
.
Теперь, подставляя эти равенства в (1),
получаем: -
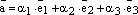 (2)
(2) -
и возможность разложения по базису доказана.
-
Линейная оболочка векторов.
-
Линейная оболочка — это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка — это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:
-
1) Если задана линейная оболочка — ранг набора векторов равен его размерности. С другой стороны в таком случае рангом или размерностью называют минимальное количество линейно независимых векторов в линейном подпространстве.
-
Векторное представление системы линейных уравнений.
-
Представим осн. матрицу А в виде в-р-столбцов А1 , А2,…, Ап.
-
Тогда система лин. ур-ний (6.1) записывается в векторном виде:
-
x1А1+х2А2+…+хnAn=b
-
А1=(
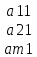 ,
)A2=(
,
)A2=(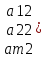 ,….
An=(
,….
An=( ),b=(
),b=(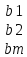 )
) -
-
Значит, сис. лин. ур-ний тхп мб представлена в виде разложения в-а b€Rm – в-ра свободных членов по n в-рам А1, А2, . . . , А п € R m – в-р-столбцам матрицы коэф., при этом коэф. разложения оказываются переменные.
-
-
-
-
-
-
-
-
-
-
-
-
Теорема Кронекера-Капелли.
-


-
-
-
-
-
-
-
Критерий линейной зависимости векторов в пространстве Rn.
-
Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
-
Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.
-
Доказательство. Необходимость. Пусть система
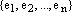 линейно
зависимая. Тогда, по определению, она
представляет нулевой вектор нетривиально,
т.е. существует нетривиальнаялинейная комбинация
данной системы векторов равная нулевому
вектору:
линейно
зависимая. Тогда, по определению, она
представляет нулевой вектор нетривиально,
т.е. существует нетривиальнаялинейная комбинация
данной системы векторов равная нулевому
вектору: -
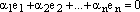 ,
, -
где хотя бы один из коэффициентов этой линейной комбинации не равен нулю. Пусть
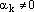 ,
, 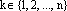 .
. -
Разделим обе части предыдущего равенства на этот ненулевой коэффициент (т.е. умножим на
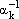 :
: -
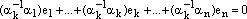 .
. -
Обозначим:
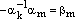 ,
где
,
где 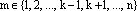 .
. -
Тогда
-
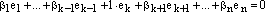
-
или
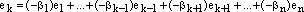 ,
, -
т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.
-
Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:
-
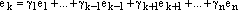 .
. -
Перенесем вектор
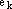 в
правую часть этого
равенства:
в
правую часть этого
равенства: -
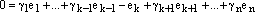 .
. -
Так как коэффициент при векторе
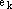 равен
равен 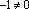 ,
то мы имеем нетривиальное представление
нуля системой векторов
,
то мы имеем нетривиальное представление
нуля системой векторов 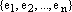 ,
что означает, что эта система векторов
является линейно зависимой, ч.т.д.
,
что означает, что эта система векторов
является линейно зависимой, ч.т.д. -
Теорема доказана.
-
Следствие.
-
1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.
-
2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.
-
Евклидовое пространство.
-
-
В математике термин евкли́дово простра́нство может обозначать один из двух сходных объектов:
-
1. Конечномерное вещественное векторное пространство
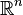 с
введённой на нём нормой
с
введённой на нём нормой -
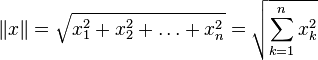
-
где
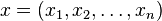 .
Также назывется конечномерным гильбертовым
пространством
.
Также назывется конечномерным гильбертовым
пространством -
2. Метрическое пространство, которое является конечномерным векторным пространством
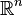 над
полемвещественных
чисел с метрикой, введённой по
формуле:
над
полемвещественных
чисел с метрикой, введённой по
формуле: -
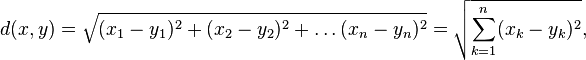
-
где
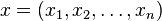 и
и 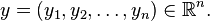
-
Наглядными примерами евклидовых пространств могут служить пространства
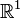 размерности n =
1 (вещественная прямая) и
размерности n =
1 (вещественная прямая) и 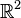 размерности n =
2 (комплексная плоскость или евклидова
плоскость).
размерности n =
2 (комплексная плоскость или евклидова
плоскость). -
-
-
-
Нормируемое пространство.
-
-
Лин. пр-во наз. нормируемым, если любому в-ру х этого пр-ва сопоставлена норма ||х|| - числа, к-рое удовл. след. св-вам:
-
1. ||х|| ≥0, если ||х|| =0, то обязательно х=0.
-
2. Для люб. вещ.числа λ €R, ||λх|| = |λ|*||x||.
-
3. Для любых 3х эл-тов x ,y ,z этого пр-ва справедливо нерав-во треуг-ника: ||x+y||= ||x||+ ||у||.
-
Если ||x||(€R) -норма х и ||x||=
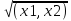 тогда
св-во 1-3 выполн.-->всякого евклидово
пр-во нормируемо.
тогда
св-во 1-3 выполн.-->всякого евклидово
пр-во нормируемо. -
-
Ортогональное дополнение и его свойства.
-
Ортог. Дополнением дан. подпр-тва наз.множество всех в-ров, ортогональных каждому в-ру из дан.подпр-ва.
-
Т.Ортог. дополние подпр-ва явл. подпр-вом.
-
Док-во. Если х ,у €
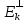 , то для любого z€Ек получим
(x,z)=0и (у,
z) = 0. Откуда следует, что и х + у
и λх €
, то для любого z€Ек получим
(x,z)=0и (у,
z) = 0. Откуда следует, что и х + у
и λх €
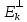 , т.к. для люб. z€Ек и λ€R по
опр.множ-ва
, т.к. для люб. z€Ек и λ€R по
опр.множ-ва
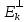 будет (
будет ( -
(х+у,z)=(x,z)+(y,z)=0+0=0и (λх,z)=(xλ,z)=λ(x,z)=0.Т.о.
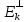 -подпр-во.
-подпр-во. -
Т.Пр-во Еп явл. прямой суммой подпр-во Ек и его ортог. дополнения.
-
Размерность ортог. дополнения к-мерного подпр-ва Ек пр-ва Еп равна п-k.
-
-
Свойства ортогонального дополнения.
-
1.(
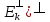 =Ek
=Ek -
Док-во.Из опред.ортог.допол.следует,что Ek c(
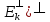 .Пусть
Ek
≠(
.Пусть
Ek
≠(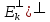 .Тогда
существ.z€(
.Тогда
существ.z€(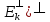 ,но
z не принадл.Ek.
En=Ek©
,но
z не принадл.Ek.
En=Ek©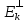 .-->существ.единств.х€
Ek,
у€
.-->существ.единств.х€
Ek,
у€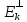 .:z=x+y.Но
(z,y)=0,т.к.
z€(
.:z=x+y.Но
(z,y)=0,т.к.
z€(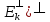 и
y€(
и
y€( .Но
и (х,у)=0, т.к. х€Ek
,y€
.Но
и (х,у)=0, т.к. х€Ek
,y€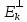 .След-но
0=(z,y)=(x+y,y)=(y,y)Что
мб при y=0.Противоречие
ч.т.д.
.След-но
0=(z,y)=(x+y,y)=(y,y)Что
мб при y=0.Противоречие
ч.т.д. -
2.Ek∩
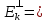 0
0 -
3.
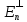 =E0
=E0 -
4.
 =En
=En -
-
-
Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение.
-
-
Пусть А – квадр. матрица. Если сущ-ет вещ. число λ, что ур-ие АХ =λ X имеет ненул. реш-е, где X – в-р-столбец, то число λ наз. собственным знач-ем, а вектор X наз.собственным в-ром матрицы А.
-
Замечая, что X = ЕХ, перепишем дан.ур-ие в виде ур-ния (А -λE )Х = 0, для к-рого по усл. необходимо найти ненул. реш-е..
-
Допустим опред. квадр. матр. (А -λЕ) отличен от 0. Тогда у неё сущ. обрат. и X = (А-λЕ)-1* 0= 0. Т. е.реше только нулевое. Сл-но собств. в-рам отвечает опред. матр. (А-λЕ)=0. Т. о. для нахождения собств. зн-ний необходимо решить ур-ие
-
|A-λE|=0(от эл-тов глав.диагонали отнимаем λ),которое наз. характеристическим ур-нием - многочлен п-степени по λ( дан. ур-ние имеет не более чем п разл. корней).
-
-
Т.Собств. вектор, соответствующий дан.собственному зн-нию, определяется с точностью до пост. множителя.
-
Док-во.Пусть X – собств. в-р матр. А , соответствующий собств. зн-нию λ, тогда АХ =λX . Возьмём произвольное вещ. число с≠0 и подействуем матр. А на в-р сХ : А (с Х )= сАХ = сλХ =λ (сХ ). Т.о. сХ - также собств.в-р матр. А с тем же собств. зн-нием. Ч.т.д.
-
Т. Если базисные в-ры явл. собств. в-рами квадр.матр. А, то эта матрица диагональна.
-
Док-во.] баз.в-р ei,i=1,..,n явл. собств.в-рами матр.А.Тогда Aei=
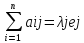 ,где(aji)=A.
Откуда aji=δjiλi,т.е.
A –это
диаг.матр.,имеющая на глав.диагонали
эл-ты λ1,λ2,…,λn.
,где(aji)=A.
Откуда aji=δjiλi,т.е.
A –это
диаг.матр.,имеющая на глав.диагонали
эл-ты λ1,λ2,…,λn. -
Т.Если собст.чЧисла λ1,λ2,…,λn , квадр. Матрицы А различны, то отвечающие им собств.в-ры en лин.незав.
-
-
Линейная функция. Билинейная форма. Квадратичная форма.
-
-
Ф-ция- это соответствие, при к-ром кажд. эл-ту v пространства V сопостав. только 1 число f(v ).
-
Ф-ция на лин. пр-ве L наз. лин., если для любых в-ров этого пр-ва х, у € L и люб. действ.числа λ€R выпол-ются равен-ва:
-
f ( x + у) = f(x) + f(y ),2. f(λx) = λ f (x ).
