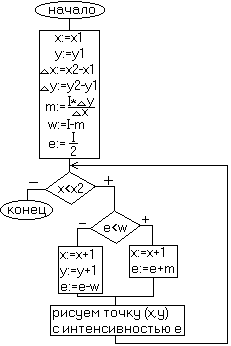
Алгоритм Брезенхема.

Этот алгоритм выбирает оптимальные растровые координаты для представления отрезка.

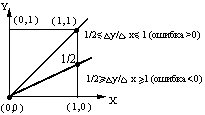
Из этого рисунка мы видим как выбирается эта координата. Сначала измеряют ошибку (обозначим её - е) отхода от линии. Затем проверяют знак ошибки: если e>0, то выбираем верхнюю пикселу, иначе нижнюю.

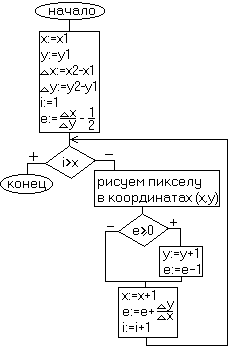
Вывод: ошибка - это интервал отсекаемый по оси y рассматриваемым отрезком в любом растровом элементе (относительно -1/2).

Пример:

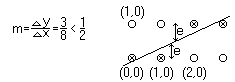
Начальные условия е:=-0.5;

m попадает в первый октант (до 45^o):

1. e = e + m = -0.5 + 3/8 = -1/8 < 0, отрезок ниже середины пиксела. e < 0, y_i = y, x_i = x + 1

2. e = e + m = -1/8 + 3/8 = 2/8 = 1/4 > 0, e > 0, y_i = y +1, x_i = x + 1, отрезок выше средней точки, так как ошибка накапливается, то ошибка сбрасывается, если она положительна по правилу: e = e - 1 = 1/4 -1 = -3/4.

3. e = e + m = -3/4 + 3/8 = -3/8 < 0 e < 0, y_i = y, x_i = x + 1

Улучшение алгоритма 1.

Много времени занимают операции: умножение и деление. Лучше работать с целыми числами и исключить деление. Чтобы избавиться от умножения, надо преобразовать декартовы координаты в экранные. Чтобы оперировать целыми числами е заменяют на

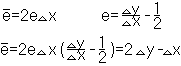
и алгоритм работает в 10 раз быстрее. Этот алгоритм даёт самую незазубренную.

Для остальных октантов:

Улучшение алгоритма 2.

Уменьшение зазубренности линий за счёт применения полутонов. Т.е. при наличии нескольких интенсивностей (оттенков требуемого цвета) внешний вид прямой может быть улучшен размыванием краев. Самый простой метод состоит в том, чтобы устанавливать интенсивность пиксела на прямой пропорционально площади части пиксела, находящейся внутри . В результате простой модификации алгоритма Брезенхема можно получить аппроксимацию площади части пиксела, находящейся внутри линии. 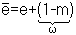Поправка к старому алгоритму: , где I - интенсивность или максимальное число градаций при переходе от чёрного к белому. Ошибка учитывает площадь, отсекаемую от пиксела.

Новый алгоритм:

Алгоритм Флойда-Стейнберга.

Алгоритм заключается в распределении ошибки по соседним пикселам (размазывание) всегда вниз и вправо. Введем понятие порога интенсивности: если интенсивность изображения превышает некую пороговую величину, то пиксел считается белым, иначе - черным. Эту величину обычно устанавливают приблизительно равной половине максимальной интенсивности, т.е.: T = I_max/2, где I_max - максимальное число градаций при переходе от чёрного к белому. T - пороговый параметр или середина диапазона градации. Если I < T, то Р_x(пиксела по х)=чёрный, ошибка = I - чёрный, иначе Р_x(пиксела по х)=белым, ошибка = I - белый,

Пиксела справа: Р_x(x+1,y) = Р_x(x+1,y) + 3/8 ошибки Пиксела снизу: Р_x(x,y+1) = Р_x(x,y-1) + 3/8 ошибки Пиксела ниже справа: Р_x(x+1,y-1) = Р_x(x+1,y-1) + 1/4 ошибки В результате исчезают резкие тени, на фотографии появляются лишние точки.

Принцип распределения: I_max = 2²

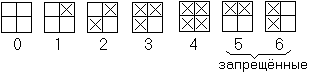
2. Геометрическое сглаживание в-сплайнами. Алгоритм.

Не все чертежи образуются исключительно набором отрезков прямых линий, окружностей и их дуг. Хорошо известный способ проведения гладкой линии, примерно проходящей через несколько заданных точек называется сглаживанием кривой типа В-сплайна. Это очень гладкая кривая или, точнее, кривая с непрерывными вторыми производными. Кривая, составленная из В-сплайнов не будет проходить точно через заданные точки. Подобную кривую составляют из дуг полиномов третьей степени, т.к. такой полином обеспечивает необходимую непрерывность.

Построение линии происходит с помощью итерационной процедуры.

Рассмотрим построение кубического сплайна. Пусть нам даны две соседние точки через которые проведём кубический полином, но у полинома - 4 коэффициента, следовательно нужно ещё два дополнительных условия или точки. Для этого прихватим ещё две соседние точки.

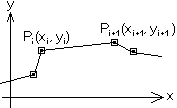
Чем более плавной мы хотим видеть линию, тем сложнее пройти точно через точки. Если в формуле x = q³, то достаточно плавности 3. Гладкость диктуется физическими задачами.

Эта линия в каждой точке имеет систему:

	x(t) y(t)	если t = 0 =< Pi t = 1 =< Pi+1	t - параметр по которому перебегаем от точки к точке.
	x(t) = ((a3 + a2)t + a1)t + a0 y(t) = ((b3 + b2)t + b1)t + b0

a₃ = (-x_i-1+ 3x_i - 3x_i+1 + x_i+2)/6 a₂ = (x_i-1 - 2x_i+ x_i+1)/2 a₁ = (-x_i-1 + x_i+1)/2 a₀ = (x_i-1 + 4x_i+ x_i+1)/6 Точки b₃ - b₀ расписывают также, но вместо x подставляют у.

Между P_i и P_i+1 точки а и b не меняются. Есди после последней точки указать первую точку, то система замкнёт контур.

Достоинства В - сплайна: между точками коэффициенты постоянны; локаьное изменение не влечет за собой вычисление заново всего сплайна.

Недостатки: могут возникать проблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности); с точки зрения эстетики не всегда приемлемы, т.к. кривизна поверхности, сконструированной с помощью сплайнов изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).