12. Зеркальное отражение.

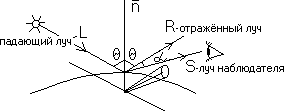
Интенсивность зеркально отраженного света зависит от угла падения, длины волны падающего света и свойств вещества. Основное уравнение Френеля приводится в любой книге по геометрической оптике. Зеркальное отражение света является направленным. Угол отражения от идеальной отражающей поверхности (зеркала) равен углу падения, в любом другом положении наблюдатель не видит зеркально отраженный свет. Это означает, что вектор наблюдения S совпадает с вектором отражения R. Если поверхность не идеальна, то количество света, достигающее наблюдателя, зависит от пространственного распределения зеркально отраженного света. У гладких поверхностей распределение узкое или сфокусированное, у шероховатых - более широкое.

В простых моделях освещения обычно пользуются эмпирической моделью Буи-Туонга Фонга, так как физические свойства зеркального отражения очень сложны. Модель Фонга имеет вид:

I_S = I_lw(i, )cosⁿ где w (i, ) — кривая отражения, представляющая отношение зеркально отраженного света к падающему как функцию угла падения i и длины волны ; n - степень, аппроксимирующая пространственное распределение зеркально отраженного света.

Свойства.

Благодаря зеркальному отражению на блестящих предметах появляются световые блики. Из-за того, что зеркально отраженный свет сфокусирован вдоль вектора отражения, блики при движении наблюдателя тоже перемещаются. Более того, так как свет отражается от внешней поверхности (за исключением металлов и некоторых твердых красителей), то отраженный луч сохраняет свойства падающего. Например, при освещении блестящей синей поверхности белым светом возникают белые, а не синие блики. На рисунке показана функция cosⁿ при - /2 <= <= /2 для различных n: большие значения n дают сфокусированные пространственные распределения характеристик металлов и других блестящих поверхностей, а малые - более широкие распределения для неметаллических поверхностей, например бумаги. 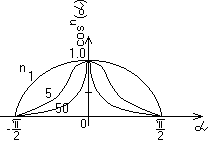Приближенные функции пространственного распределения для зеркального отражения.

Коэффициент зеркального отражения зависит от угла падения, однако даже при перпендикулярном падении зеркально отражается только часть света, а остальное либо поглощается, либо отражается диффузно. Эти соотношения определяются свойствами вещества и длиной волны. Коэффициент отражения для некоторых неметаллов может быть всего 4%, в то время как для металлических материалов - более 80%. На первом рисунке, показанном ниже, коэффициенты отражения для типичных веществ при нормальном падении света показаны как функции длины волны, а на рисунке рядом - как функции угла падения. Обратите внимание, что при падении под скользящим углом ( = 90°) отражается весь падающий свет (коэффициент отражения 100%). Кривые отражения.

Модель освещения.

Объединяя эти результаты с формулой рассеянного света и диффузного отражения, получим модель освещения:

I = I_ak_a + (I_l/(d+K))(k_dcos + w(i, )cosⁿ )

Функция w (i, ) довольно сложна, поэтому ее обычно заменяют константой k_s, которая либо выбирается из эстетических соображений, либо определяется экспериментально. Таким образом,

I = I_ak_a + (I_l/(d+K))(k_dcos + k_Scosⁿ )

В машинной графике эта модель часто называется функцией закраски и применяется для расчета интенсивности или тона точек объекта или пикселов изображения. Чтобы получить цветное изображение, нужно найти функции закраски для каждого из трех основных цветов. Константа k_s обычно одинакова для всех трех основных цветов, поскольку цвет зеркально отраженного света определяется цветом падающего. Если имеется несколько источников света, то их эффекты суммируются. В этом случае модель освещения определяется как

I = Iaka +

(Ili/(d+K))(kdcos i + kScosni i)

где m - количество источников.

Применяя формулу скалярного произведения двух векторов, запишем cos = (nL)/|n||L|=n'L' где n' и L' - единичные векторы соответственно нормали к поверхности и направления к источнику. Точно так же cos = (RS)/|R||S|=R'S' где R' и S' - единичные векторы, определяющие направления отраженного луча и наблюдения. Следовательно, модель освещения для одного источника определяется как I = I_ak_a + (I_l/(d+K))[k_d(n'L') + k_S(R'S')ⁿ]

Попробуйте сами составить простую модель освещения с такими данными: предположим, что на верхнем рисунке в точке Q поверхности векторы нормали, падающего света и наблюдения следующие: n=j L = -i + 2j - k S = i + 1.5j + 0.5k пусть на сцене находится только один объект, d = 0, К = 1 и интенсивность источника будет в 10 раз больше, чем интенсивность рассеянного света, т. е. I_a = 1, а I_l = 10. Объект имеет блестящую металлическую поверхность, поэтому в основном свет будет отражаться зеркально. Пусть k_s = 0.8, k_a = k_d = 0.15 и n = 5. Заметим, что k_s + k_d = 0.95, т. е. 5% энергии источника поглощается.

Построим вектор отражения R: R = i + 2j + k

Определяя элементы модели освещения, получаем

n'L'=(nL)/|n||L|=(j*(-i+2j-k))/((-1)²+2²+(-1)²)^1/2=2/(6^1/2)

или =cos^-1(2/(6^1/2))=32.26⁰

и R'S'=(RS)/|R||S|=[(i+2j+k)(i+1.5j+0.5k)]/[(1²+2²+1²)^1/2*(1²+1.5²+0.5²)^1/2]=4.5/(6^1/2*3.5^1/2)=4.5/(21^1/2)

или =cos^-1(4.5/(21^1/2))=10.89⁰

Окончательно

I = (1)(0.15) + (10/1)[(0.15)(6)^1/2 + (0.8)(4.5/(21)^1/2)⁵] = 0.15 + 10(0.12 +0.73) = 8.65

Вектор наблюдения почти совпадает с вектором отражения, поэтому в точке Q наблюдатель видит яркий блик. Однако при изменении положения наблюдателя, например, если

S = i +1.5j - 0.5k

то R'S'=(RS)/|R||S|=3.5/(21^1/2) и =40.2⁰

В этом случае I = 0.15 + 10(0.12 + 0.21) = 3.45 и яркость блика в точке Q значительно ослабевает.