22. Вынужденные колебания. Дифференциальное уравнение вынужден-

ных колебаний системы и его решение. Период и амплитуда вынужденных

колебаний. Сдвиг фаз между смещением и вынуждающей силой.

Для получения незатухающих колебаний необходимо обеспечить компенсацию потерь энергии колебаний с помощью какого - либо внешнего источника. Рассмотрим процесс осуществления незатухающих колебаний при воздействии на реальную колебательную систему внешнего источника гармонической силы F_вн = F_мcos t. Как и ранее, используем силовой подход, основывающийся на втором законе Ньютона mа = F_.

Результирующая сила F_ действующая на груз массой m, включает в себя:

F_ = F_упр + F_сопр + F_вн = - kх – r + F_мcos t

Рассматриваем одномерный случай, проектируя векторное равенство 2 - го за­кона Ньютона на некоторую ось х: mx" = - kх – rх' + F_мcos t  х" + 2(r2m)х' + (km)х = F_мcos t  х" + 2х^ + _о²х = (F_мm) cos t

Получили дифференциальное уравнение вынужденных гармонических колеба­ний (ДУВГК), где: r,  = r 2m и _о = (k/m), как и раньше - коэффициент сопротивления, коэффициент затухания и циклическая частота свободных колебаний груза на пружине, соответственно.

Полученное уравнение является неоднородным, то есть - с не нулевой правой частью, независящей от переменной х и навязывающей ей определённый, а именно - гармонический характер изменения. Решение неоднородного дифференциального уравнения представляется суммой решений соответствующего однородного уравнения (с искусственно полагаемой нулю правой частью) и частного решения неоднородного уравнения.

Решения: х = Аcos (t – ); А = F_мm[(_о² - ²)² + 4²²]; tg  = 2(_о² - ²).

Амплитуда и частота вынужденных колебаний оказываются частотно-зависи­мыми, зависящими от частоты , т. е. от быстроты изменения вынуждающей силы и соотношения её с частотой _о свободных колебаний груза на пружине.

Зависимость (), называемая фазочастотной характеристикой колеба­тельной системы

23. Вынужденные колебания. Амплитуда вынужденных колебаний. Ре-

зонанс.

А

мплитуда А вынуж­денных колебаний, как пока­зывает анализ полученного для нее выражения, зависит от час­тоты вынуждающей силы и коэффициента зату­хания. Графически характер зави­симости А() для разных значений коэффициента затухания представлен на чертеже.

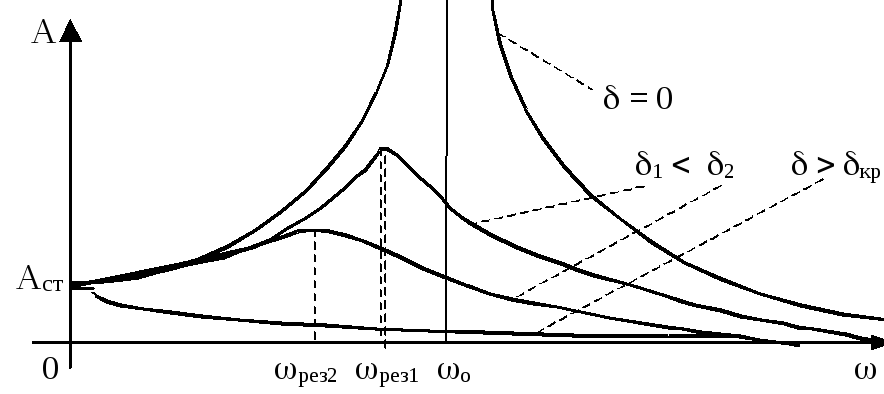
Обращает на себя внимание наличие максимумов на этих зависимостях при значениях коэффициента затухания не превышающих некото­рого критического, равного _кр = _о2. При больших затуханиях   _кр амплитуда вынуж­денных колебаний монотонно убывает с ростом частоты вынуждающей силы.

На низких частотах   _о имеем так называемый статический случай; соответствующее (статическое) значение амплитуды вынужденных колебаний равно: А_ст = F_мm_о² = F_мk. (Напомним, что _о² = k/m).

Явление возрастания амплитуды вынужденных колебаний при изменении час­тоты вынуждающей силы называется резонансом. Значение резонансной ампли­туды определим из условия экстремума зависимости A().

Из dАd = 0   = _рез = (_о² - 2²) и А_рез = F_м2m(_о² – ²)

При нулевом затухании резонанс происходит точно на частоте _о свободных колебаний системы, а значение резонансной амплитуды равно А_рез = F2m_о = . Нет ограниче­ния для "раскачки" вынужденных колебаний.

Затухание понижает резонансную частоту и понижает значение резонанс­ной амплитуды вынужденных колебаний/ резонанс "тупеет" и "левеет"/.

Явление резонанса представляет собой эффект являющийся амплитудно-фазовым эффектом. На некоторой частоте  = _р вынуждающая сила оказывается сфазированной со скоростью вынужденных колебаний и в течение всего периода колебаний действует "по скорости"  = dr/dt и, соответственно, "по перемещению dr" вынужденных колеба­ний, осуществляя их максимальную раскачку. При таком фазовом синхронизме, когда внешняя сила действует "в такт" вынужденным колебаниям; она совершает максимальную работу и развивает наибольшую мощность  = F_вын.

Можно также считать, что при  = _р вынуждающая сила действует в противофазе с силой сопротивления и, совершая максимальную работу, максимально повышает амплитуду (и энергию) вынужденных колебаний.

При резонансе колебательная система отбирает от внешнего источника мак­симальную мощность. Это и есть фундаментальный признак резонанса.