
- •Основы вычислительной математики Учебно-методическое пособие
- •Оглавление
- •Предисловие
- •I. Введение
- •Контрольные вопросы
- •II. Системы линейных алгебраических уравнений
- •II.1. Основные понятия и определения
- •II.2. Прямые методы решения систем линейных уравнений
- •II.3. Метод Гаусса решения слау
- •II.4. Решение слау с помощью -разложения
- •II.5. Метод итераций решения слау
- •II.6. Метод Зейделя решения слау
- •II.7. Сходимость итерационных процессов для систем линейных уравнений
- •III. Методы решения нелинейных скалярных уравнений
- •III.1. Локализация корней
- •III.2. Метод простых итераций
- •III.3. Приведение нелинейного уравнения к виду , допускающему сходящиеся итерации
- •III.4. Метод Ньютона (Метод касательных)
- •III.5. Контрольные вопросы
- •III.6. Задачи для самостоятельного решения
- •IV. Приближенное решение систем нелинейных уравнений
- •IV.1. Метод Ньютона
- •IV.2. Метод итераций
- •IV.3. Контрольные вопросы
- •IV.4. Задачи для самостоятельного решения
- •V. Интерполяция и аппроксимация
- •V.1. Интерполяция
- •V.2. Интерполяционный многочлен в форме Лагранжа
- •V.3. Интерполяционный многочлен в форме Ньютона
- •V.4. Приближение методом наименьших квадратов
- •V.5. Контрольные вопросы
- •V.6. Задания для самостоятельного решения
- •VI. Равномерное приближение функций
- •V.1. Полиномы Чебышева
- •VI.2. Понятие о равномерном приближении функций
- •VI.3. Контрольные вопросы
- •VII. Приближенное дифференцирование
- •VII.1. Постановка вопроса
- •VII.2. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона
- •VII.3. Формулы приближенного дифференцирования, основные на формуле Стирлинга
- •VII.4. Контрольные вопросы
- •VII.5. Задачи для самостоятельного решения
- •VIII. Численное интегрирование функций
- •VIII.1. Общие замечания
- •VIII.2.Квадратурные формулы Ньютона-Котеса
- •VIII.3. Формула трапеций и ее остаточный член
- •Общая формула трапеций (правило трапеций).
- •VIII.4. Формула Симпсона и ее остаточный член
- •Общая формула Симпсона (параболическая формула).
- •VIII.5. Формулы Ньютона-Котеса высших порядков
- •VIII.6. Контрольные вопросы
- •VIII.7. Задачи для самостоятельного решения
- •IX. Приближенное решение обыкновенных дифференциальных уравнений
- •IX.1. Интегрирование дифференциальных уравнений с помощью степенных рядов
- •IX.2. Метод последовательных приближений
- •IX.3. Метод Эйлера
- •IX.4. Метод Эйлера с итерациями
- •IX.5. Метод Рунге-Кутта
- •IX.6. Контрольные вопросы
- •IX.7. Задачи для самостоятельного решения
- •X. Преобразование фурье
- •X.1. Разложение периодических функций в ряд Фурье
- •X.2. Эффект Гиббса
- •X.3. Контрольные вопросы
- •IX.4. Задачи для самостоятельного решения
- •Список литературы
II.6. Метод Зейделя решения слау
Метод
Зейделя представляет собой некоторую
модификацию метода итерации. Основная
его идея заключается в том, что при
вычислении
![]() -го
приближения неизвестной
учитываются уже вычисленные ранее
-е
приближения неизвестных
-го
приближения неизвестной
учитываются уже вычисленные ранее
-е
приближения неизвестных
![]() .
Пусть дана приведенная линейная система
.
Пусть дана приведенная линейная система
.
Выберем
произвольно начальные приближения
корней
![]() ,
стараясь, чтобы они в какой-то мере
соответствовали неизвестным
,
стараясь, чтобы они в какой-то мере
соответствовали неизвестным
![]() .
Далее, предполагая, что
-ые
приближения
.
Далее, предполагая, что
-ые
приближения
![]() корней известны, согласно методу Зейделя
будем строить
-ые
приближения корней по следующим формулам:
корней известны, согласно методу Зейделя
будем строить
-ые
приближения корней по следующим формулам:
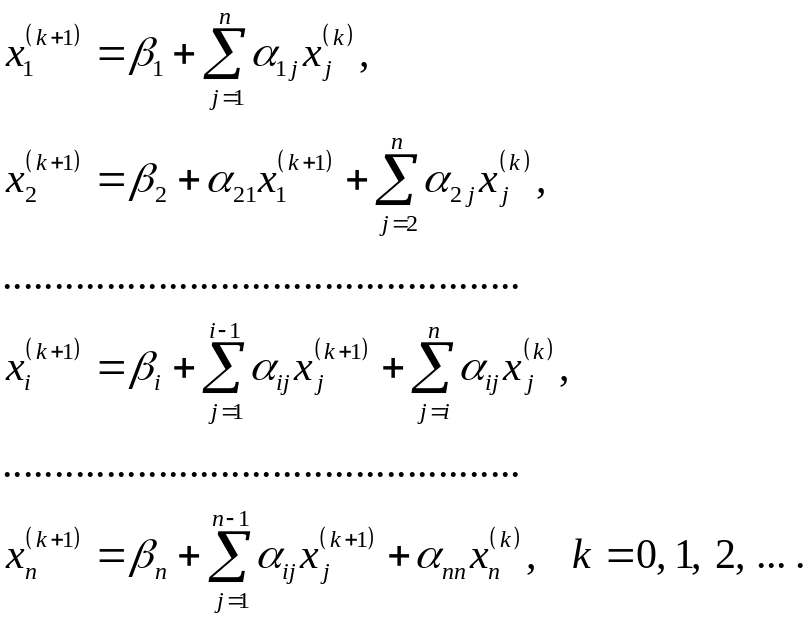
Теорема сходимости для простой итерации остается верной и по методу Зейделя.
Пример 2.4. Методом Зейделя решить систему

Решение. Приведем систему к виду, удобному для итерации

В качестве нулевых приближений корней возьмем:
![]()
Применяя метод Зейделя, последовательно получим


и т.д.
Результаты вычислений с точностью до четырех знаков поместим в таблицу:
|
|
|
|
0 |
1,2000 |
0,0000 |
0,0000 |
1 |
1,2000 |
1,0600 |
0,9480 |
2 |
0,9992 |
1,0054 |
0,9991 |
3 |
0,9996 |
1,0001 |
1,0001 |
4 |
1,0000 |
1,0000 |
1,0000 |
5 |
1,0000 |
1,0000 |
1,0000 |
Точные значения корней: .
II.7. Сходимость итерационных процессов для систем линейных уравнений
Определение
2.1. Под нормой
матрицы
понимают действительное число
![]() ,
удовлетворяющее условиям:
,
удовлетворяющее условиям:
1.
![]() ,
причем
,
причем
![]() .
.
2.
![]() ,
– число, в частности,
,
– число, в частности,
![]() .
.
3.
![]() .
.
4.
![]() .
.
В дальнейшем для матрицы произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы:
1.
 (
-норма);
(
-норма);
2.
![]() (
(![]() -норма);
-норма);
3.
 (
-норма).
(
-норма).
Пример 2.5. Пусть
 .
.
Имеем



В
частности, для вектора
![]() эти нормы имеют следующий вид:
эти нормы имеют следующий вид:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Пусть имеем приведенную линейную систему
, (2.19)
где
![]() ,
,
![]() – заданные матрицы,
– искомый вектор.
– заданные матрицы,
– искомый вектор.
Теорема 2.3. Процесс итерации для приведенной линейной системы (2.19) сходится к единственному решению, если какая-нибудь каноническая норма матрицы меньше единицы, т.е. для итерационного процесса
![]()
(![]() – произвольно) достаточное условие
сходимости есть
– произвольно) достаточное условие
сходимости есть
![]() .
.
Следствие. Процесс итерации для системы (2.19) сходится, если
1.
 или
или
2.
![]() или
или
3.

Пусть
![]() и
и
![]() – два последовательных приближения
решения линейной системы
– два последовательных приближения
решения линейной системы
.
Приведем оценку погрешности приближений процесса итерации:
 ,
(2.20)
,
(2.20)
где
![]() и
и
![]() какие-нибудь канонические нормы матриц
и
какие-нибудь канонические нормы матриц
и
![]() .
.
Пример 2.6. Показать, что для системы

процесс
итерации сходится. Сколько итераций
следует выполнить, чтобы найти корни
системы с точностью до
![]() ?
?
Решение. Приведя систему к специальному виду, получим

Отсюда матрица системы

Используя,
например, норму
![]() ,
получим:
,
получим:
![]() .
.
Следовательно, процесс итерации для заданной системы сходится. За начальное приближение корня примем

Отсюда
![]()
Пусть – число итераций, необходимое для достижения заданной точности. Применяя формулу (2.20), имеем
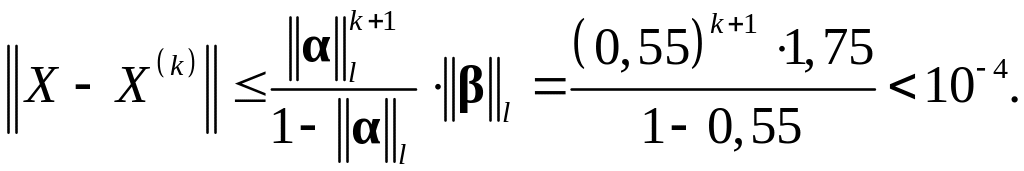
Отсюда
 ,
,
![]() ,
,
![]() .
.
Следовательно,
 и
и
![]() .
.
Можно
принять
![]() .
.
II.8. Контрольные вопросы
Прямые методы решения систем линейных алгебраических уравнений (СЛАУ).
Метод Гаусса решения СЛАУ.
Метод -разложения решения СЛАУ.
Метод итераций решения СЛАУ.
Достаточные условия сходимости метода итераций.
Метод Зейделя решения СЛАУ.
Сходимость итерационных процессов.
II.9. Варианты индивидуальных заданий
1. Решить системы линейных алгебраических уравнений методом Гаусса и методом -разложения.
1.1.
 1.2.
1.2.

1.3.
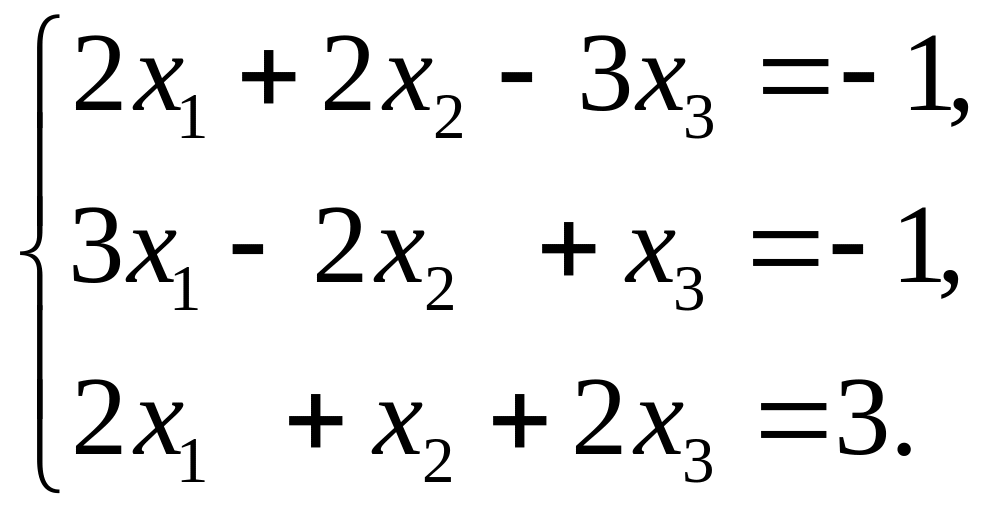 1.4.
1.4.

1.5.
 1.6.
1.6.

1.7.
 1.8.
1.8.
1.9.
 1.10.
1.10.

1.11.
 1.12.
1.12.

1.13.
 1.14.
1.14.

1.15.

2. Следующие системы линейных алгебраических уравнений решить методом итераций и методом Зейделя, проделав в каждом из методов по четыре итерации.
2.1.
 2.2.
2.2.

2.3.
 2.4.
2.4.

2.5.
 2.6.
2.6.

2.7.
 2.8.
2.8.

2.9.
 2.10.
2.10.

2.11.
 2.12.
2.12.

2.13.
 2.14.
2.14.
2.15.

