X.2. Эффект Гиббса
Эффект Гиббса возникает при решении задачи синтеза для разрывных функций. Изучим основные его проявления на примере прямоугольной импульсной функции
которая
имеет скачек, равный 1 в точке разрыва
.
Формальное разложение в ряд Фурье
находится подстановкой функции
в формулы (10.8), вычислением интегралов,
оказывающихся равными
и подстановкой выражений для коэффициентов в (10.9):
Использование конечного числа членов ряда приводит к тому, что частичные суммы ряда, являются функциями, в которых присутствуют периодические составляющие. Их период равен периоду последнего удержанного члена или первого оставленного.
К. Ланцош предложил способ уменьшения эффекта пульсаций за счет сглаживания усеченного ряда
(8.18)
интегрированием (усреднением) по периоду последнего оставленного члена.
При
выборе в качестве интервала сглаживания
периода последнего члена усеченного
ряда Фурье сглаженное значение
получим как среднее от
:
(10.19)
На практике берется как номер первого отбрасываемого члена ряда.
Подставляя (10.18) в (10.19), получим:
Применяя известные тригонометрические формулы, окончательно находим:
(10.20)
где
– так называемые сигма-факторы:
(10.21)
Таким
образом, сглаженный ряд Фурье есть
исходный ряд Фурье с коэффициентами,
умноженными на соответствующие
сигма-факторы. Отметим, что эффект
сглаживания достигается за счет того,
что при
сигма-фактор
-го
члена
оказывается равным нулю.
С
физической точки зрения формулу (10.20)
можно трактовать как наблюдение исходной
функции
через узкое просвечивающее прямоугольное
окно шириной
.
Наблюдаемая функция
есть средняя интенсивность света от
исходной функции
.
Она оказывается более яркой, когда
функция
больше, и менее яркой, когда функция
меньше.
X.3. Контрольные вопросы
Ортогональные функции.
Ряд Фурье для периодической Функции.
Различные формы записи для ряда Фурье.
Эффект Гиббса.
IX.4. Задачи для самостоятельного решения
Разложить заданную периодическую функцию в ряд Фурье. Построить на одном чертеже график исходной функции и ее аппроксимирующих полиномов .
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
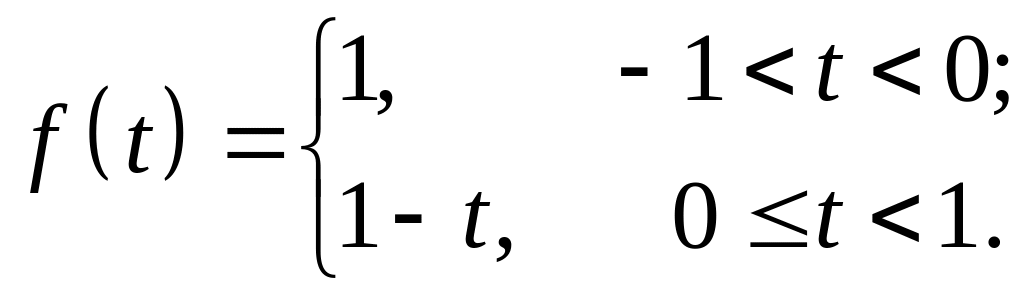14.
15.
Список литературы
Пирумов У.Г. Численные методы: Учеб. Пособие для студ. втузов. – М.: Дрофа, 2003. – 224 с.
Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высш. шк., 2002. – 840 с.
Поршнев С.В. Вычислительная математика. Курс лекций. – СПб.: БХВ-Петербург, 2004. – 320 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2002. – 632 с.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа: Учеб. Пособие для студ. втузов. – М.: Изд-во «Наука», 1967. – 368 с.
Демидович Б.П., Марон И.А. Основы вычислительной математики: Учеб. Пособие для студ. втузов. – М.: Изд-во «Наука», 1970. – 664 с.