1.2.3. Ценность информации и ее эффективность.

Мате­матическая теория информации полностью игнорирует содержание информации. Поэтому вопрос о ее ценности не ставится. Рассчиты­вая пропускную способность канала связи, бессмысленно принимать во внимание содержание телеграмм.

Вопрос о ценности возникает прежде всего в биологии. Биоло­гическая эволюция необратима и направленна. Исходный материал для эволюции — случайные мутации генов — не имеют заданной на­правленности, тем не менее работает мощный направляющий фак­тор — естественный отбор, основанный на повышении ценности ин­формации, трансформированной в итоге мутации. Таким образом, для биологии существенна не столько количественная, сколько цен­ностная характеристика информации. На это одним из первых обра­тил внимание И. Шмальгаузен [103].

Информация может быть более или менее ценной в зависимости, от преследуемой цели, происхождение которой до недавнего времени в теории информации не обсуждалось. Ценной информацией считается та, которая помогает достижению цели.

Следует обратить внимание на следующее различие оценок "ко­личество" и "ценность". В отличие от шенноновского определения количества информации, передаваемой по каналам связи, ценность проявляется в результатах рецепции. Она непосредственно связана с рецепцией. Ю.А. Шрейдеру принадлежит следующий наглядный пример: "Имеется том 2 'Курса высшей математики'В.И. Смир­нова. Эта книга содержит богатую информацию. Какова ее цен­ность? В ответ приходится спросить — для кого? Для дошкольника ценность этой информации нулевая, так как он не обладает достаточ­ной подготовкой, достаточным уровнем рецепции и не в состоянии эту информацию воспринять. Для профессора математики ценность тоже нулевая, так как он все это хорошо знает. Максимальной цен­ностью эта информация обладает для студентов того курса, кото­рым книга предназначена, поскольку речь идет об очень хорошем учебнике. Зависимость ценности от уровня подготовки, от предше­ствующего запаса информации — тезауруса... — проходит через мак­симум" [51, с. 158, 159]. Это иллюстрируется рис. 1.6.

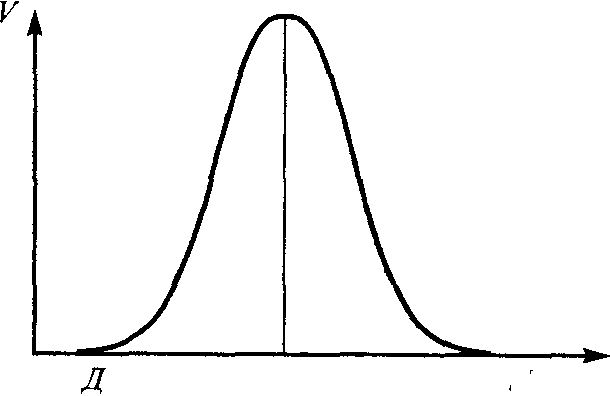
С П Тезаурус

Рис. 1.6. Зависимость ценности информации от тезауруса; Д — дошкольник, С — студент, П — профессор

Известны несколько способов количественного определения ценно­сти. Все они основаны на представлении о цели, достижению которой способствует полученная рецептором информация. Чем в большей мере информация помогает достижению цели, тем более ценной она считается.

1. Если цель наверняка достижима, и притом несколькими пу­тями, то возможно определение ценности (V) по уменьшению мате­риальных или временных затрат благодаря использованию информа­ции. Так, например, сочетание хороших предметного и алфавитного каталогов библиотеки, наличие библиографических справочников со­кращают время на составление списка литературы по конкретному интересующему читателя вопросу.

2. Если достижение цели не обязательно, но вероятно, то исполь­зуется один из следующих критериев:

а) мерой ценности, предложенной М.М. Бонгартом [22] и А.А. Харкевичем [183], является величина

где р — вероятность достижения цели до получения информации, а Р — после; учитывая, что р и Р могут изменяться от 0 до 1, заключим, что пределы изменения V — от —оо до +оо;

б) мерой ценности, предложенной В.И. Корогодиным [76, с. 5], является величина

при этом V изменяется от 0 до 1.

Очевидно, величину V для некоторой информации невозможно за­дать одним единственным числом. Определенное значение ценности можно получить только лишь для известной пары источник—рецеп­тор (например, учебник—студент).

Ценность информации, получаемой рецептором, зависит от ее ко­личества. Так, если целью изучения учебника является овладение ме­тодом решения определенного цикла задач, то прочтение двух-трех параграфов в лучшем случае дает возможность решать лишь малую долю задач. С ростом количества информации увеличивается вели­чина V.

В области малых значений I скорость увеличения V мала в силу изложенных выше соображений, но и в области больших / темп роста уменьшается, поскольку, начиная с некоторых значений I, дальней­ший рост этой величины уже не влияет на успех решения задач из цикла: любая задача может быть решена. Это значит, что кривая V = /(/) для данной пары источник—рецептор имеет вид кривой с насыщением (рис. 1.7).

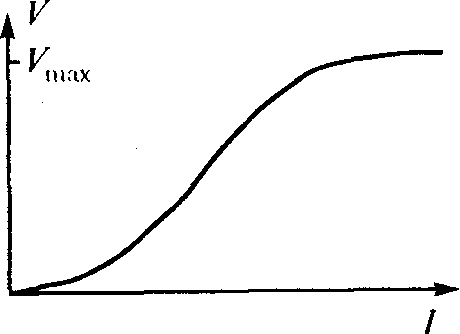
Рис. 1.7. Зависимость ценности информации от ее количества

Рис. 1.8. Зависимость эффективности информации (Е) от ее количества (/);