1 курс / ОТК 1 курс-20191213T204228Z-001 / ОТК / Л_тература по ОТК / otksp_STZI_press для диска

6.4 Перехідні процеси у колах R, C; R, L; R, L, C при синусоїдній дії

6.4.1 Увiмкнення джерела синусоїдної дiї до кола R, C

При увімкненні синусоїдної дії перехідні процеси значною мірою залежать від фази напруги (струму) джерела в момент комутації.

Нехай коло R, C (рис.6.16, а) вмикається до джерела синусоїдної напруги e(t) = Em cos(ωt +ψE ) за нульових початкових умов: uC (−0) = 0 .

Якщо необхідно визначити закон змінювання напруги на ємності, можна скористатись рівнянням (6.39), яке в даному випадку матиме вигляд:

dt

Диференціальному рівнянню (6.69) відповідає характеристичне:

RCp +1 = 0 .

Рисунок 6.16 – Кола, які вмикаються до джерела синусоїдної напруги

За класичним методом розв’язок рівняння (6.69) можна знайти, як

uC (t) = uC вл(t) +uC вм(t) ,

де uCвл(t) = Ae−t /τ , p1 = −1/ RC = −1/ τ.

Оскiльки дiя є синусоїдною, вимушена складова визначається методом комплексних амплiтуд:

Визначивши A, можна записати кінцевий вираз для шуканої напруги:

Отже, напруга на ємностi дорівнює сумі двох складових. Залежно вiд величини ψUС спостерігаються два характерних випадки.

1. Нехай в момент увiмкнення джерела миттєве значення вимушеної складової дорiвнює нулю. Це можливо, якщо ψUС = ±π/ 2 . Тодi cos ψUС = 0 ,

uC вл(t) = 0 і перехiдних процесiв не виникає.

2. У загальному випадку, коли ψUC ≠ π/ 2 ; cos ψUC ≠ 0 , напруга на

ємностi, як це видно з (6.70), може суттєво вiдрiзнятися вiд напруги вимушених коливань uC вм(t) . Найхарактернішим у цьому сенсі є перехiдний процес, який

спостерiгається при ψUС = 0, π (рис.6.17, а).

У нульовий момент часу сума напруг uC вл(t) +uC вм(t) = 0 . Потiм виникає

перехiдний процес, який закiнчується через 4,6τ. При t > 4,6τ вiльна складова практично дорiвнює нулю i графiк uC (t) збігається з кривою uC вм(t) . Пiсля замикання ключа через промiжок часу Tвл / 2 , напруга uC (t) >UmC . Отже,

максимум напруги на ємностi може перевищувати амплiтуду вимушеної складової майже удвічі (особливо, якщо стала часу велика).

Рисунок 6.17 – Графіки струмів і напруг при увімкненні до джерела синусоїдної напруги кіл: а – R, C; б – R, L

6.4.2 Увiмкнення джерела синусоїдної дiї до кола R, L

Оскільки дія змінюється за синусоїдним законом, вимушену складову струму знаходять методом комплексних амплiтуд:

початковий момент часу вимушена складова струму дорiвнює нулю, вiльний струм вiдсутнiй, i у колi вiдразу встановлюється стацiонарний стан.

2. У загальному випадку вимушена складова струму у початковий момент вiдрiзняється вiд нуля, i у колi спостерiгається перехiдний процес (рис.6.17, б). З рисунка видно, що у початковий момент часу перехiдний струм помiтно вiдрiзняється за формою вiд вимушеного струму iвм(t) , причому у деяких

точках його перебiльшує.

Максимально можливi значення струму у колi, як це виходить з формули (6.71), спостерiгаються, коли вимушена складова у момент часу t = +0 досягає максимуму, тобто при ψE = ϕ, або ψвм = ψE −ϕ = 0, ± π. Якщо стала часу

велика, то на iнтервалi, де t << τ, максимуми струму наближаються до 2Im .

6.4.3 Увiмкнення джерела синусоїдної дiї до кола R, L, C

Нехай послідовне коло R, L, C (рис.6.16, в) вмикається до джерела синусоїдної дiї e(t) = Em cos ωt за нульових початкових умов.

Оскільки пiсля комутацiї утворюється коло (див. п.6.3.4), можна

(6.45). З точки зору забезпечення вибірних властивостей кіл найважливішим є випадок комплексно-спряжених коренiв, що вiдповiдає високому значенню добротностi (Q >>1), а отже, явищу резонанса. Тодi

uСвл(t) = Ae−δt cos(ωвлt +ψU ) ; uС(t) = Ae−δt cos(ωвлt +ψU ) +uСвм(t) .

Вимушена складова напруги визначається комплексним методом:

яка з огляду на закони комутації за нульових початкових умов матиме вигляд:

Отже, uC (t) є сумою двох коливань з рiзними частотами. Аналiзуючи

формулу (6.79), можна зробити висновок, що характер перехiдних процесiв залежить вiд спiввiдношення мiж частотою коливань зовнiшньої дiї ω i

резонансною частотою ωрез . Можливі три випадки: 1) ∆ω = 0 , δ ≠ 0 ; 2) ∆ω ≠ 0 ,

δ= 0 ; 3) ∆ω ≠ 0 , δ ≠ 0 , де ∆ω= ω−ωрез − абсолютна розстройка.

1.При ∆ω = 0 , ω= ωрез вираз (6.79) перетворюється так:

uС(t) = −UmCe−δt cos(ωрезt +ψUС ) +UmC cos(ωрезt +ψUС ) =

де umС(t) = EmQ(1−e−δt ) − рiвняння обвідної.

У даному випадку амплiтуда коливань напруги на ємностi контуру зростає у часі за експоненцiйним законом, наближаючись до значення EmQ .

Щоб знайти швидкiсть зростання амплiтуди коливань, необхідно розрахувати похiдну dumC (t) / dt = EmQδe−δt у початковий момент часу:

Отже, швидкiсть зростання обвідної не залежить вiд значення добротностi. Тому у контурi з вищою добротнiстю (Q2 > Q1 ) для встановлення

стацiонарного режиму потрiбен бiльший час ( tуст2 > tуст1 , рис.6.18, а). Осцилограма напруги на ємностi при увімкненні синусоїдної напруги в момент t = 0 та при вимкненнi в момент t =ti (що еквівалентно дії прямокутного

радіоімпульса тривалістю ti ) зображена на рис.6.18, б.

2. Якщо частота зовнiшнiх коливань ω не збігається з резонансною частотою і контур не має втрат ( δ = 0 ), напруга на ємностi, як це виходить з виразу (6.79), є сукупнiстю двох гармонiчних коливань, котрі мають близькi частоти i приблизно однаковi амплiтуди. Тоді

uС(t) = −UmC cos(ωрезt +ψUC ) +UmC cos(ωt +ψUC ) =

У результатi пiдсумовування вiльної i вимушеної складових виникають так званi биття (рис.6.19). З рiвняння (6.81) виходить, що обвідна umC (t)

повiльно змiнюється у часі за законом:

umC (t) = 2UmC sin ωрез2−ωt ,

а частота коливань дорiвнює (ω +ωрез) / 2 ω .

0

t

Рисунок 6.19 – Графік напруги на ємності за умови ω ≠ ωрез, δ → 0

Биття матимуть подвоєну амплiтуду, оскiльки у випадку однакових фаз векторiв UC вл i UC вм , цi вектори спрямованi однаково, i тому їх амплiтуди

пiдсумовуються. Перiод биттiв розглядають як величину, що у два рази менша перiоду синусоїди, тобто Tб = 2π / ωрез −ω .

3. У реальному контурi (коли δ ≠ 0 ) величина вiльної складової uC вл(t)

зменшується за експоненцiйним законом. Внаслiдок цього при ∆ω ≠ 0 i δ ≠ 0 в результаті підсумовування двох коливань uC вм(t) і uC вл(t) з близькими

частотами також виникають биття, але обвідна перехiдного процесу матиме складніший вигляд (рис.6.20), ніж у попередньому випадку (рис.6.19).

Щоб пояснити форму обвідної, слiд розглянути векторну дiаграму напруг (рис.6.21, а, б). Вектори U mC вм і U mC вл обертаються в комплексній площині

проти годинникової стрілки з різними кутовими швидкостями ω і ωрез

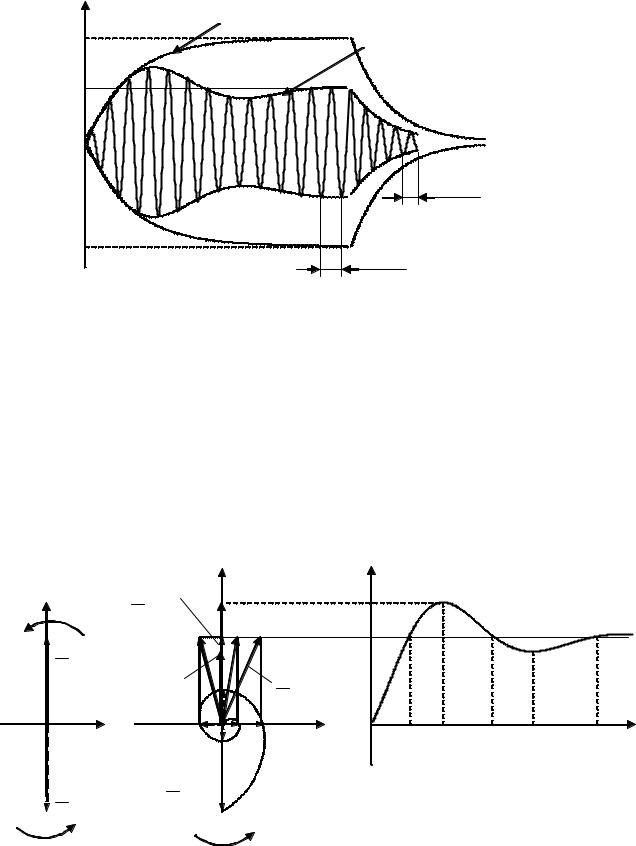
відповідно (нехай ωрез > ω). При t = 0 , як виходить з формули (6.79), ці вектори перебувають у протифазі (рис.6.21, а).

0 t

2π/ ωрез

2π/ ω

Рисунок 6.20 – Графік напруги на ємності в колі R, L, C за умови ω ≠ ωрез, δ ≠ 0 при дії прямокутного радіоімпульсу

Якщо обертати систему координат із швидкістю ω за годинниковою стрілкою, то вектор U mC вм буде нерухомим, а вектор U mC вл − обертатиметься

із швидкістю ωрез −ω. Вектор результуючого коливання U mC дорівнює геометричній сумі векторів U mC вм і U mC вл (рис.6.21, б). Його кінець описує на площині загасаючу спіраль (якщо δ = 0 , то – коло радіуса UmC вл ), а сам він

хитається, змінюючись як за величиною, так і за початковою фазою (а отже, і за частотою). Проекція вектора U mC на вісь ординат відтворює закон змінювання

обвідної umC (t) за часом (рис.6.21, в).

6.5 Запитання та завдання для самоперевірки

іконтролю засвоєння знань

1.За яких умов у колі виникають перехідні процеси?

2.Сформулювати закони комутації. Зобразити схеми заміщення індуктивності та ємності за нульових початкових умов.

3.Пояснити фізичний сенс сталої часу для R, L і R, C кіл. Як залежить стала часу від величини R для кожного з цих кіл?

4.Як визначити порядок кола? Чи залежить вигляд характеристичного рівняння від функції, яка діє на вході кола?

5.Які існують способи складання характеристичного рівняння?

6.Який зв'язок існує між КПФ і диференціальним рівнянням кола?

7.У чому полягає класичний метод аналізу перехідних процесів? Пояснити поняття вільної та вимушеної складових струму (напруги).

8. Під час дії джерела постійної напруги e(t) = E =120 В у колі (рис.6.3, а) після замикання перемикача встановився усталений режим. Визначити напругу на конденсаторі через t1 = 0,1с після розмикання перемикача, якщо C = 2 мкФ,

R1 = R2 =50 кОм.

Відповідь: uC (t1) = 23В.

9. Опір R = 50 Ом та незаряджена ємність C = 5 мкФ, які з’єднані послідовно, увімкнено при t = 0 до джерела ЕРС E = 20В. Знайти струм у колі.

Відповідь: i(t) = 0,4e−4000t А.

10. Послідовно з’єднані індуктивність L =1 мГн і опір R =100 Ом вмикають при t = 0 до джерела синусоїдної напруги e(t) = 20 cos(105 t + π/ 4) В. Знайти напругу uL (t) та побудувати графік.

Відповідь: uL (t) =14,1e−100000t +14,1cos(105 t + π/ 2) В.

11.Чи може частота коливального розряду ємності в контурі R, L, C дорівнювати або перевищувати резонансну частоту цього контуру?

12.Обчислити частоту незагасаючих ωрез та вільних ωвл коливань

e(t) = 200sin(1000t + ψE ) В. У момент t = 0 , коли напруга джерела, збільшуючись,

досягає додатного значення, що дорівнює діючому, розмикається перемикач. Знайти iL (t) , uC (t) , якщо: L =50 мГн, C = 20 мкФ, R1 = R2 =50 Ом.

Відповідь: iL (t) = −1,41e−1000t + 2,82sin1000t А; uC (t) = 70,7e−1000t В.

Рисунок 6.23 – Схеми електричних кіл

ЧАСОВІ ХАРАКТЕРИСТИКИ КІЛ

•Перехідна характеристика кола

•Імпульсна характеристика кола

•Часові характеристики типових кіл R, L; R, C; R, L, C