36. Операция вставки элемента в в-дерево. Проблема переполнения, методы решения. Пример.

В-дерево – это сбалансированное многоходовое дерево. Особенностью В-дерева является то, что каждая вершина не должна содержать ровно N ключей; вершины В-дерева могут иметь свободное пространство, используемое для вставки новых элементов. Такая организация дерева упрощает операции вставки и удаления.

Название «В-дерево» можно объяснить двумя способами:

а) от слова Balanced – сбалансированное дерево, в котором все листья имеют один и тот же уровень;

б) от Bayer – автора данной структуры.

Введем определение В-дерева. В-деревом степени t называется структура, обладающая следующими свойствами:

1. Все пути от корня до любых листьев имеют одинаковую длину h, называемую также высотой В-дерева.

2. В каждой вершине дерева, за исключением корня, должно располагаться минимум n-1, максимум 2n-1 ключей.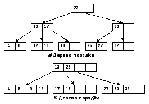

3. В корне В-дерева может располагаться минимум 1, максимум 2n-1 ключей.

4. Любая вершина дерева, за исключением листьев, имеющая j ключей, должна иметь j+1 подчиненную вершину.

Последнее условие означает, что промежуточные вершины В-дерева имеют от n до 2n указателей на подчиненные вершины, а корень дерева – от 2 до 2n указателей.

Таким образом, степень В-дерева определяет степень его «пустоты» (или заполнения) – минимальное количество включенных в В-дерево элементов (или максимальное количество свободных позиций). Нижняя граница гарантирует, что вершины В-дерева заполнены, по крайней мере, наполовину. Верхняя граница позволяет определить регулярную структуру каждой вершины В-дерева.

Степень дерева влияет на эффективность доступа: чем выше степень дерева, тем ниже само дерево, а значит, тем меньше обращений к внешней памяти потребуется для поиска элемента.

Структура вершины В-дерева Обозначим записи, размещенные в одной вершине дерева, через R₁, R₂, …, R_j, а указатели на подчиненные вершины через P₀, P₁, P₂, …, P_j. Тогда структура вершины будет следующей: P₀ R₁ P₁ R₂ P₂ … P_j-1 R_j P_j

Правила следования:

1. Ключи записей в текущей вершине упорядочены по возрастанию, т.е. ключ записи R₁ меньше ключа записи R₂, который, в свою очередь, меньше ключа записи R₃, и т.д.

2. Записи в подчиненной вершине, на которую указывает P₀, имеют ключи, меньшие, чем ключ записи R₁.

3. Записи в подчиненной вершине, на которую указывает P_j, имеют ключи, большие, чем ключ записи R_j.

4. Записи в подчиненной вершине, на которую указывает P_i (0 < i < j), имеют ключи, большие, чем ключ записи R_i, и меньшие, чем ключ записи R_i+1.

Поиск в В-дереве очень похож на поиск в бинарном дереве поиска, но с тем отличием, что если в бинарном дереве поиска мы выбирали один из двух путей, то здесь предстоит сделать выбор из большего количества альтернатив, зависящего от того, сколько дочерних узлов имеется у текущего узла. Точнее, в каждом внутреннем узле х нам предстоит выбрать один из 2t дочерних узлов.

Пояснения к алгоритму поиска.

Результат успешного поиска – указатель на узел дерева и положение искомого ключа в данном узле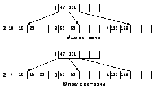

Результат не успешного поиска – NULL значение указателя.

Обозначения: k – искомый ключ; x (изначально) – указатель на корень дерева.

Просмотр ключей узла дерева осуществляется так:

key₀ < key₁ < … < key_{n – 1}

цикл по i = 0, 1, …, n – 1 и k > key_i

Если k < key₀ (i = 0), должен быть выбран ptr₀

Если k > key_{i – 1} и k < key_i, должен быть выбран ptr_i

Если k > key_{n – 1}, должен быть выбран ptr_n, или опять же ptr_i, так как здесь i = n

Операции вставки предшествует поиск, который должен завершиться не успешно.

Операция вставки позволяет включить новый элемент только в лист В-дерева. Поэтому, прежде всего, определяется целевая вершина – лист В-дерева, куда должен быть вставлен новый элемент, не нарушая упорядоченности записей.

Когда целевая вершина (лист) В-дерева будет найдена, можно столкнуться со следующими ситуациями.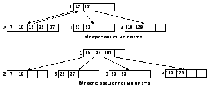

1. Простейший случай, когда найденный лист имеет свободные позиции (не заполнен полностью). В этом случае новый элемент вставляется в найденный лист, не нарушая упорядоченности ключей.

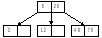
Пусть, например, имеется следующий фрагмент В-дерева порядка 2. Необходимо вставить элемент с ключом 7. Новый элемент должен быть размещен в листе с номером 2, в котором есть свободные позиции. В результате выполнения операции вставки получим новое В-дерево.

2. Случай переполнения вершины: найденный целевой лист заполнен полностью. При вставке нового элемента в целевой лист получим последовательность из 2n+1 ключей, тогда как в листе могут находиться максимум 2n ключей. В этом случае выполняется операция расщепления листа: ключ из средней позиции переносится в родительскую вершину, а на уровне листьев появляются два новых листа.

Рассмотрим пример. Пусть в представленное выше дерево порядка 2 вставляется элемент с ключом 37. Поэтому получим последовательность ключей: 7, 10, 15, 23, 37. В средней позиции находится элемент с ключом 15; он перемещается в родительскую вершину, и появляются два новых листа.

Когда элемент перемещается в родительскую вершину, для нее также рассматриваются эти же две ситуации. Если родительская вершина заполнена полностью, для нее также выполняется операция расщепления с перемещением элемента на вышерасположенный уровень. В результате высота дерева может увеличиться на 1.

Рассмотрим пример вставки нескольких значений в В-дерево порядка 1.

Пусть вставляется следующая последовательность элементов: 20, 12, 48, 3, 5, 70, 101.

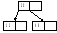
1. Первые два элемента заполняют первый лист, который является одновременно и корнем В-дерева.

2. Вставляется следующий элемент – 48. Получаем переполнение: 12, 20, 48. Элемент из средней позиции поднимается вверх и создает новую вершину – корень В-дерева, которой подчинены два листа

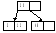
3. Элемент с ключом 3 вставляется в самый левый лист

4. Элемент с ключом 5 также должен быть вставлен в самый левый лист; получаем переполнение – 3, 5, 12, и элемент из средней позиции перемещается в родительскую вершину, в которой есть свободное место.

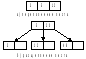
5. Следующий элемент (70) вставляется в самый правый лист, в котором есть свободная позиция.

6. В тот же лист должен быть вставлен следующий элемент с ключом 101; получаем переполнение – 48, 70, 101, и элемент из средней позиции перемещается в родительскую вершину. В родительской вершине также возникает переполнение – 5, 20, 70; в результате перемещения элемента из средней позиции образуется новая вершина – корень В-дерева , и высота дерева увеличивается на 1.

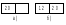
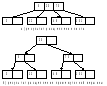
Процесс вставок можно продолжать, включая в дерево новые элементы.

Таким образом, при вставке элементов в дерево В-дерево растет вверх – появляется новый корень, хотя новый элемент вставляется в лист дерева.