39. Основные свойства оценок

О.1. Оценку параметра называют несмещённой, если её математическое ожидание равно оцениваемому параметру , то есть . Если это равенство не выполняется, то оценка может либо завышать значение , либо занижать его. В обоих случаях это приводит к систематическим ошибкам в оценке параметра. Требование несмещённости гарантирует отсутствие систематических ошибок при оценке параметров.

О.2. Несмещённую оценку , которая имеет наименьшую дисперсию среди всех несмещённых оценок параметра , вычисленных по выборкам одного и того же объёма, называют эффективной оценкой.

О.3. Оценку параметра называют состоятельной, если она подчиняется закону больших чисел, то есть при достаточно большом числе независимых наблюдений п с вероятностью, близкой к единице, можно утверждать, что разность между и по абсолютной величине окажется меньше сколь угодно малого числа , или , где - положительное число, близкое к нулю.

На практике при оценке параметров не всегда удаётся удовлетворить одновременно требованиям несмещённости, эффективности и состоятельности оценки. Так, например, может оказаться, что для простоты расчётов целесообразно использовать незначительно смещённую оценку. Однако выбору оценки всегда должно предшествовать её критическое рассмотрение со всех точек зрения.

40. Оценка математического ожидания и дисперсии

Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают математическое ожидание и дисперсию.

Т.1. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной Х, которая имеет математическое ожидание , является несмещённой оценкой этого параметра.

Доказательство. Пусть независимые наблюдения над случайной величиной. По определению . Найдём 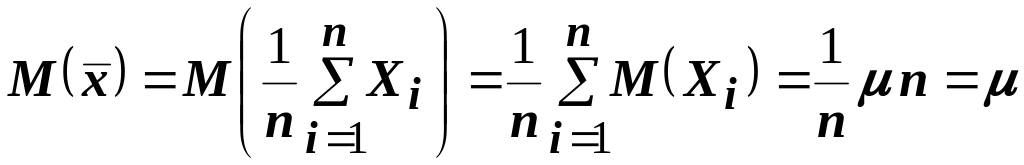. Следовательно: .

Т.2. Средняя арифметическая , вычисленная по п независимым наблюдениям над случайной величиной, которая имеет математическое ожидание и дисперсию , является состоятельной оценкой этого параметра.

Доказательство. Вычислим

.

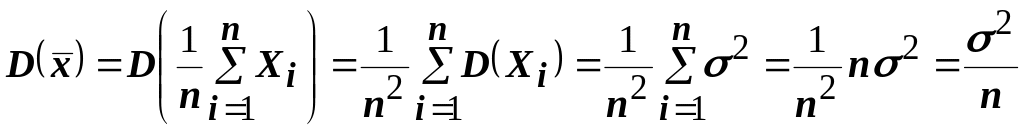Запишем неравенство Чебышева для средней арифметической , или . При достаточно большом числе испытаний величина является числом, близким к нулю. Поэтому для сколь угодно малого числа выполняется неравенство , определяющее свойство состоятельности выборочных оценок.

Получение эффективных оценок - сложное дело. Приведём без доказательства важный для практики факт. Если случайная величина Х распределена по нормальному закону с параметрами , то несмещённая оценка математического ожидания имеет минимальную дисперсию , поэтому средняя арифметическая в этом случае является эффективной оценкой математического ожидания .

Т.3. Если случайная выборка состоит из п независимых наблюдений над случайной величиной Х с математическим ожиданием и дисперсией , то выборочная дисперсия не является несмещённой оценкой генеральной дисперсии.

Доказательство. По условию и тогда

Упростим выражение 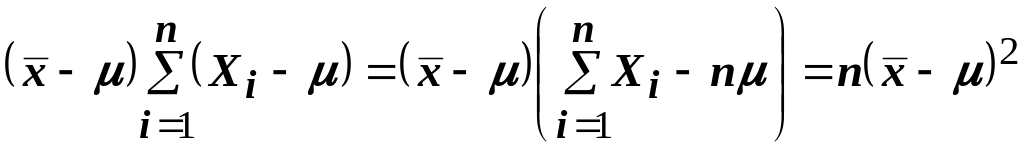, подставив полученное в выражение для эмпирической дисперсии получим

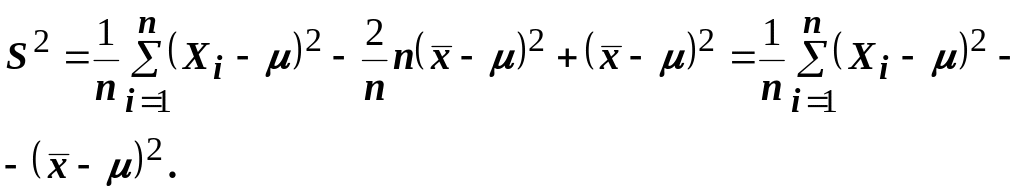
Но так как 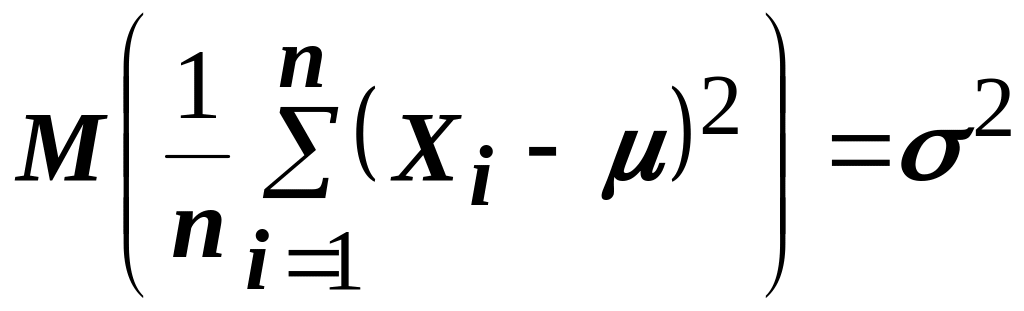и то 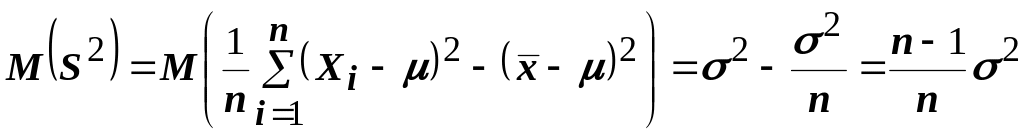. То есть является смещённой оценкой дисперсии генеральной совокупности.

Несмещённой оценкой дисперсии генеральной совокупности является . Обычно эту оценку называют исправленной выборочной дисперсией. Дробь называют поправкой Бесселя. Тогда имеем равенство . При малых значениях п поправка Бесселя довольно сильно отличается от единицы, с увеличением п она быстро стремится к единице. При практически нет разницы между и . Можно показать, что оценки и являются состоятельными оценками .

Несмещённой, состоятельной и эффективной оценкой является оценка , для вычисления которой необходимо знать математическое ожидание. Заметим, что оценка эффективна лишь при условии нормальности распределения случайной величины Х в генеральной совокупности. Оценки и не являются эффективными. В том случае, когда значение математического ожидания неизвестно, то для оценки дисперсии используют состоятельную и несмещённую оценку .