2. Математическое программирование.
2.1. Решение уравнений
Многие инженерные и экономические задачи сводятся к исследованию функций одной или нескольких переменных вида Y=f(X) или Y=f(x1,x2,…xN). Исследовать функцию – значит установить область ее существования (те значения Х при которых возможно вычислить Y), определить области значений Х, при которых Y принимает положительные, отрицательные и аномально большие значения ("уходит в бесконечность"), найти максимумы, минимумы, асимптоты, иногда – точки перегиба графика функции, а также корни уравнения Y= f(x) – значения х, при которых Y обращается в 0 (график функции пересекает ось абсцисс).
Наиболее простые методы исследования функциональных зависимостей с помощью компьютера – итерационные, основанные на многократном выполнении сравнительно простых операций. Один из итерационных методов – табулирование функции (расчет значений Y при заданных X) в большом диапазоне значений Х с большим шагом, затем табулирование с небольшим шагом в наиболее интересных диапазонах – вблизи корней, максимумов и минимумов, далее – сужать диапазоны Х и уменьшать шаг для получения все более точных значений экстремумов и корней. Более эффективен метод касательных: вычисляется Y0=f(X0) и производная в этой точке, проводится касательная; точка пересечения касательной и оси Х принимается за следующее приближение к корню X1, вычисляется Y1=f(X1) и т.д. Получаемые решения зависят от того, в каких диапазонах Х и Y ведется их поиск, т.е. от их начальных значений. На рисунке 1 показано приближение к различным корням в зависимости от начальных условий. Для многомерных задач используется многомерный аналог производной – градиент: вектор, указывающий направление самого быстрого возрастания функции многих переменных. Движение вдоль градиентов позволяет за несколько шагов (итераций) подойти достаточно близко к корню, максимуму или минимуму функции. В частности, на этом основан метод Ньютона.
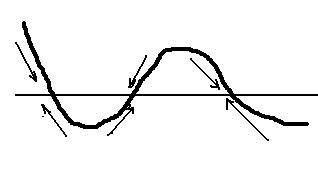
Рис.2.1. Приближение к различным корням уравнения
в зависимости от начальных условий.
Различные итерационные методы разрабатывались начиная с XVIII века, и в настоящее время имеется большое количество компьютерных программ для их использования. Наиболее простые и удобные программы оформлены в виде функций Excel "Подбор параметра" и "Поиск решения". Но необходимо помнить, что для нелинейных моделей результаты расчётов зависят от начальных значений Х (опорного плана), решений может быть несколько, и компьютер может не найти решение, даже если оно существует.
Основная цель планирования любой деятельности – получение максимального результата (прибыли, объема производства и т.п.) при имеющихся ограничениях. Разработке оптимальных программ-планов посвящен раздел математики под названием “математическое программирование”, в частном случае – “линейное программирование”. Стандартная формулировка задачи математического программирования: изменяя значения аргументов, требуется найти минимум или максимум зависящей от них целевой функции, наиболее полно характеризующей эффективность экономической деятельности, при наложенных ограничениях-равенствах и ограничениях-неравенствах. Допустимое решение, отвечающее этим условиям, называется оптимальным планом. Его может не существовать, если наложенные ограничения противоречивы, а иногда может существовать множество решений. В задачах линейного программирования целевая функция и функции в ограничениях – линейные.
Для решения задач линейного программирования используются различные методы (Ньютона, наискорейшего спуска, симплекс-метод), общий принцип которых таков: выбирается неоптимальный опорный план, и его параметры варьируются с целью последовательного улучшения плана, то есть оптимизации целевой функции при соблюдении всех ограничений, с использованием сервиса Поиск решения, что дает возможность решать оптимизационные задачи, не вникая в сложную математику.