Системы счисления. Алгоритмы перевода чисел.
Представление чисел в двоичном коде
Чтобы работать с данными различных видов, необходимо унифицировать форму их представления, а это можно сделать с помощью кодирования. Проблемами универсального кодирования занимаются различные области науки техники, культуры. Вспомним, что чертежи, ноты, математические выкладки являются тоже некоторым кодированием различных информационных объектов. Аналогично, универсальная система кодирования требуется для того, чтобы большое количество различных видов информации можно было бы обработать на компьютере
Подготовка данных для обработки на компьютере (представление данных) в информатике имеет свою специфику, связанную с электроникой. Например, мы хотим проводить расчеты на компьютере. При этом нам придется закодировать цифры, которыми записаны числа. На первый взгляд, представляется вполне естественным кодировать цифру ноль состоянием электронной схемы, где напряжение на некотором элементе будет равно 0 вольт, цифру единица – 1 вольт, двойку – 2 вольт и т.д., девятку – 9 вольт. Для записи каждого разряда числа в этом случае потребуется элемент электронной схемы, имеющий десять состояний. Однако элементная база электронных схем имеет разброс параметров, что может привести к появлению напряжения, скажем, 3,5 вольт, а оно может быть истолковано и как тройка и как четверка, т.е. потребуется на уровне электронных схем объяснить компьютеру, где заканчивается тройка, а где начинается четверка. Кроме того, придется создавать весьма непростые электронные элементы для производства арифметических, операций с числами, т.е. на схемном уровне должны быть созданы таблица умножения – 10x10 = 100 схем и таблица сложения – тоже 100 схем. Для электроники 40-х гг. (время, когда появились первые вычислительные машины) это была непосильная задача. Еще сложнее выглядела бы задача обработки текстов, ведь русский алфавит содержит 33 буквы. Очевидно, такой путь построения вычислительных систем не состоятелен.
В то же время весьма просто реализовались электронные схемы с двумя устойчивыми состояниями: есть напряжение – 1, нет напряжения – 0, есть электрическое (магнитное) поле – 1, нет – 0. Взгляды создателей вычислительной техники были обращены на двоичное кодирование как универсальную форму представления данных для дальнейшей обработки их средствами вычислительной техники. Предполагается, что данные располагаются в некоторых ячейках, представляющих упорядоченную совокупность из двоичных разрядов, а каждый может временно содержать одно из состояний — 0 или 1. Тогда группа из двух двоичных разрядов (двух бит) может закодировать 22= 4 различные комбинации кодов (00 01 10 11); аналогично, восемь бит или 1 байт – 28 = 256 и т.д.
Существуют различные способы записи чисел, например: можно записать число в виде текста – сто двадцать три; римской системе счисления СХХШ; арабской — 123.
Системы счисления
Совокупность приемов записи и наименования чисел называется системой счисления.
Числа записываются с помощью символов, и по количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская. Например, для записи числа один используется буква I, два и три выглядят как совокупности символов II, III, но для записи числа пять выбирается новый символ V, шесть – VI, десять — вводится символ X, сто – С, тысяча – М и т.д. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.
Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим q.
В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q = 10, т.е. используется 10 цифр: 0 1 2 3 4 5 6 7 8 9.
Число в позиционной системе счисления с основанием q может быть представлено в виде полинома по степеням q. Например, в десятичной системе мы имеем число
123,45 = 1 102+ 2 101+ 3 100+ 4 10-1+ 5 10-2,
Записывая слева направо цифры числа, мы получим закодированную запись числа в q-ичной системе счисления.
В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, q = 2 . На ранних этапах развития вычислительной техники арифметические операции с действительными числами производились в двоичной системе ввиду простоты их реализации в электронных схемах вычислительных машин.
А значит, для реализации поразрядной арифметики в компьютере потребуются вместо двух таблиц по сто правил в десятичной системе счисления две таблицы по четыре правила в двоичной. Соответственно на аппаратном уровне вместо двухсот электронных схем – восемь.
Но запись числа в двоичной системе счисления длиннее записи того же числа в десятичной системе счисления в log210 раз (примерно в 3,3 раза). Это громоздко и не удобно для использования, так как нормальный объем человеческого внимания составляет примерно три-четыре объекта, т.е. удобно будет пользоваться такими системами счисления, в которых наиболее часто используемые числа (от единиц до тысяч) записывались бы одной-четырьмя цифрами. Как это будет показано далее, перевод числа, записанного в двоичной системе счисления, в восьмеричную и шестнадцатеричную очень сильно упрощается по сравнению с переводом из десятичной в двоичную. Поэтому, наряду с двоичной системой счисления, в информатике имеют хождение восьмеричная и шестнадцатеричная системы счисления.
Восьмеричная система счисления имеет восемь цифр: 0 12 3 4 5 6 7. Шестнадцатеричная – шестнадцать, причем первые 10 цифр совпадают по написанию с цифрами десятичной системы счисления, а для обозначения оставшихся шести цифр применяются большие латинские буквы, т.е. для шестнадцатеричной системы счисления получим набор цифр: 0123456789ABCDEF.
Если из контекста не ясно, к какой системе счисления относится запись, то основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:
231(10)=11100111(2)=347(8)=Е7(16). Запишем начало натурального ряда в десятичной, двоичной, восьмеричной и шестнадцатеричной системах .
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
А |
|
11 |
1011 |
13 |
В |
|
12 |
1100 |
14 |
С |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
Е |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
|
17 |
10001 |
21 |
11 |
|
Преобразование чисел из одной системы счисления в другую
Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.
Рассмотрим алгоритм на примере перевода десятичного числа 231 в двоичную систему (совершенно аналогичен перевод из десятичной системы в любую q-ичную). Разделим число на два (основание системы): нацело 231 : 2 = 115 и остаток 1, далее 115: 2 = 57 и остаток 1, и т.д. до получения 1.
Таким образом, последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.
231 = 1 х27+ 1 х26+ 1 х25+ 0 х 24+0 х 23+ 1 х 22+ 1 х 21 +1х20 = 11100111(2).
Эти выкладки можно сократить, записав процесс деления следующим образом:
231 \2
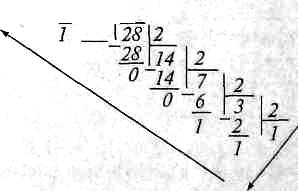
231(|0)=11100111(2)
Читая частное и остатки от деления в порядке, обратном получению, получим двоичную запись числа. Такой способ перевода чисел называется правилом (алгоритмом) последовательного делении, очевидно, что он применим для любого основания.
Между двоичной системой счисления, с одной стороны, и восьмеричной и шестнадцатеричной (заметим 8 и 16 – есть третья и четвертая степени двойки) – с другой, существует связь, позволяющая легко переводить числа из одной системы в другую.
Для перевода в шестнадцатеричную систему счисления сгруппируем целую и дробную части в группы по четыре цифры (они называются тетрадами), и каждую группу независимо от других перевести в одну шестнадцатеричную цифру.
Аналогичное правило для восьмеричной системы, используя группировку по три цифры.
