2. Корреляционно-регрессионный анализ математических моделей

2.1. Понятия корреляции и регрессии

Корреляция в переводе с латинского обозначает соответствие или взаимосвязь. Корреляционная зависимость отражает связь между величинами, когда определенным значениям факториальных величин соответствует много значений зависимой величины.

Корреляционный анализ в задачах моделирования транспортных процессов и систем имеет фундаментальное значение, так как теснота корреляционной связи определяет структуру модели. Высокая и полная корреляционная связь требует объединения величин. Отсутствие или слабость корреляционных связей позволяют рассматривать величину как независимую.

Во многих случаях выбор независимых величин на базе исследования их корреляционных связей требует дополнительного экспертного исследования и решения.

Например, при формировании имитационной модели (см. пример 1.2 и рис. 1.1) независимость источников грузопотоков между собой, а также и получателей грузов между собой требует корреляционного анализа. При наличии зависимости (например, дополнительных перевозок грузов между источниками грузопотоков) требуются изменение структуры имитационной модели, учет этих связей.

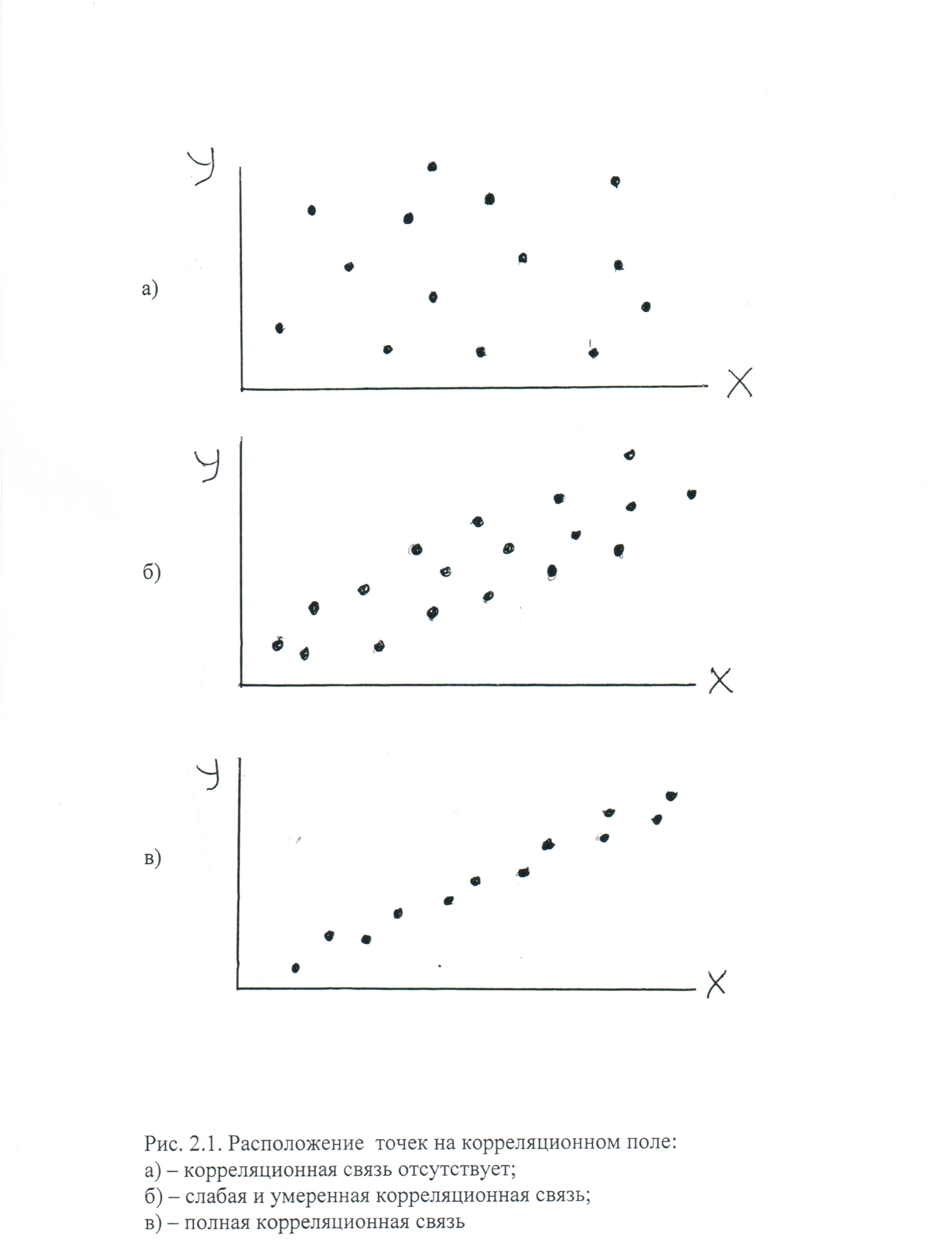
Корреляционная связь между двумя переменными изучается с помощью парной корреляции. О тесноте корреляционной связи можно судить по характеру расположения точек на графике, связующем переменные х и у. Такой график называется полем корреляции (рис. 2.1). Разброс точек по всему полю свидетельствует об отсутствии корреляции (рис. 2,а), рис. 2,б свидетельствует о слабой умеренной корреляции, рис. 2,в - о полной корреляции.

Численное значение корреляционной связи оценивается коэффициентом корреляции r.

Задачей регрессионного анализа является установление вида зависимости (1.2) (зависимости параметра оптимизации у от факториальных величин х₁, х₂…х_n). Указанная зависимость называется уравнением регрессии. Корреляционно-регрессионный анализ позволяет прогнозировать развитие рассматриваемого явления и решать задачу построения модели и ее оптимизации. Регрессионный анализ введен в практику расчетов английским математиком и механиком У.Р. Гамильтоном в 1840-х годах.

При проведении регрессионного анализа применяются понятия парных и множественных коэффициентов регрессии. На рис. 2.2 показано корреляционное поле парной линейной зависимости, отказов автомобилей в эксплуатации от числа капитальных ремонтов. Рассмотрение расположения точек на поле рис. 2.2 позволяет говорить о слабой корреляционной зависимости, разброс точек на рис. 2.2 примерно соответствует рис. 2.1,б. Из рис. 2.2 видно, что если для каждой величины х найти средние значения у и соединить эти точки, то получится ломанная линия, называемая опытной линией регрессии. Очевидно, что полученная линия является следствием ошибок замеров, недостаточного их количества, дискретности графика. По мере увеличения числа данных (увеличения объема выборки) ломаная линия асимптотически приближается к какой-то плавной кривой. Поскольку объем данных всегда ограничен, то возникает задача аппроксимации опытной линии регрессии теоретической функцией. Функция, аппроксимирующая опытную ломаную линию, называется теоретической линией регрессии.

При парной зависимости опытная линия регрессии может быть аппроксимирована с помощью следующих функций:

у = а + b х – прямая линия;

у = а х² + b х + с – парабола второго порядка;

у = – гипербола;

у = а + b lg х – логарифмическая функция.

Используются также показательная и степенная функции, арифметическая и геометрическая прогрессии, алгебраический полином, тригонометрический ряд (ряд Фурье) и другие функции.

В общем случае для n переменных уравнение регрессии приобретает более сложный вид.