76)Теорема Кронекера-Капелли.

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA*.

Очевидно, что система (1) может быть записана в виде:

x1 + x2 + … + xn

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

78)Каноническое уравнение окружности.

Окружность – множество всех точек плоскости, равноудаленных от данной точки на плоскости.

Выведем уравнение окружности.

Пусть C(a, b) – центр окружности, а R – ее радиус. Возьмем произвольную точку M(x, y) принадлежит окр.

Расстояние от центра окружности до точки M находится по известной формуле

Каноническое уравнение окружности. В центре с координатами a и b и радиусом R

Если в этом уравнении раскрыть скобки и выполнить некоторые преобразования, то получим:

Приведение уравнения окружности к каноническому виду:

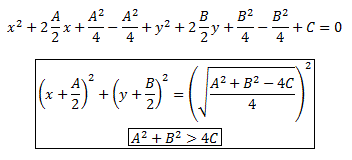
80)Каноническое уравнение параболы. Геометрический смысл коэффициентов.

Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:

y^2=2px

Действительно, введем прямоугольную систему координат. Вершину параболы примем за начало системы координат; прямую, проходящую через фокус перпендикулярно директрисе, примем за ось абсцисс (положительное направление на ней от точки к точке ); прямую, перпендикулярную оси абсцисс и проходящую через вершину параболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат оказалась правой).

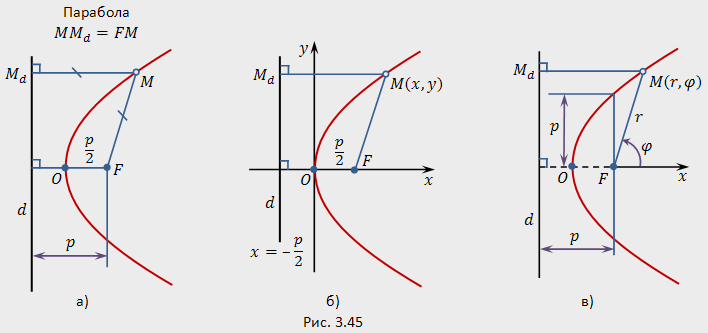
Составим уравнение параболы, используя её геометрическое определение, выражающее директориальное свойство параболы. В выбранной системе координат определяем координаты фокуса и уравнение директрисы x=-p/2.

Каноническое уравнение параболы y^2=2*p*x.

т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.51), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, аналитическое определение параболы эквивалентно его геометрическому определению, выражающему директориальное свойство параболы.

82)Формулировка основной теоремы алгебры.

Основна́я теоре́ма а́лгебры утверждает, что

Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.

Эквивалентная формулировка теоремы следующая:

Поле комплексных чисел алгебраически замкнуто.

Теорема, утверждающая, что любой многочлен с комплексными коэффициентами имеет корень в поле комплексных чисел. А. о. т. была высказана впервые А, Жираром и Р. Декартом в формулировке, отличной от современной. К. Маклорен и Л. Эйлер уточнили формулировку А. о. т., придав ей форму, эквивалентную современной: всякий многочлен с действительными коэффициентами можно разложить в произведение линейных и квадратичных множителей с действительными коэффициентами. Ж. Д'Аламбер первым в 1746 опубликовал доказательство А. о. т. Во 2-й пол. 18 в. появляются доказательства Л. Эйлера, П. Лапласа, Ж. Лагранжа и др. Во всех этих доказательствах предполагается заранее, что какие-то «идеальные» корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. К. Гаусс первый доказал А. о. т. без предположения, что корни существуют. Его доказательство, по существу, содержит построение поля разложения многочлена. Во всех доказательствах А. о. т. используются в той или иной форме топологич. свойства действительных и комплексных чисел. Роль топологии была сведена в конечном итоге к единственному предложению, согласно к-рому многочлен с действительными коэффициентами нечетной степени имеет действительный корень.