50)Условие совпадения двух прямых в пространстве.

1. Две прямые параллельны или совпадают тогда и только тогда, когда их направляющие векторы коллинеарные.

2. Две прямые перпендикулярны тогда и только тогда, когда их направляющие векторы ортогональны.

52)Условие скрещивающихся прямых в пространстве.

Как известно , прямые l1 и l2 называются скрещивающимися, если они не лежат в одной плоскости. Пусть а и b — направляющие векторы этих прямых, а точки M1 и M2 принадлежат соответственно прямым и l1 и l2 (рис. 208).

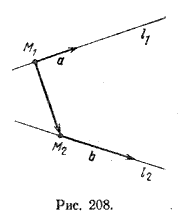Тогда векторы а, b, M1M2> не компланарны, и поэтому их смешанное произведение не равно нулю, т. е. (а, b, M1M2> ) =/= 0.

Верно и обратное утверждение:

если (а, b, M1M2> ) =/= 0, то векторы а, b, M1M2> не компланарны, и, следовательно, прямые l1 и l2 не лежат в одной плоскости, т. е. скрещиваются.

Таким образом, две прямые скрещиваются тогда и только тогда, когда выполнено условие

(а, b, M1M2> ) =/= 0, (1)

где а и b — направляющие векторы прямых, а M1 и M2 — точки, принадлежащие соответственно данным прямым. Условие

(а, b, M1M2> ) = 0 (2)

является необходимым и достаточным условием того, что прямые лежат в одной плоскости. Если прямые заданы своими каноническими уравнениями

то а = (а1; а2; а3), b = (b1; b2;b3), М1 (x1; у1; z1), М2(х2; у2; z2) и условие (2) записывается следующим образом:

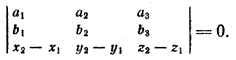
54)Условие параллельности прямой и плоскости.

Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, но не являющиеся параллельными.

Пример скрещивающихся прямых — транспортная развязка, здесь верхняя дорога — это одна прямая, а идущая под ней дорога — скрещивающаяся с первой вторая прямая, высота опоры моста примерно равна расстоянию между этими двумя прямыми.

56)Условие ортогональности прямой и плоскости.

Прямая а перпендикулярна плоскости α, если она перпендикулярна двум пересекающимся прямым b и с этой плоскости.

Если прямые b и с, принадлежащие плоскости α, расположены произвольно относительно плоскостей проекций, то прямые углы между прямой а и прямыми b и с спроецируются на плоскость проекций с искажениями. Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. е. являться соответственно горизонталью и фронталью плоскости α..

Прямая а перпендикулярна плоскости α, если она перпендикулярна пересекающимся горизонтали h и фронтали f этой плоскости.

При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений.

Кроме вышесказанного существует теорема:

Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция − к фронтальной проекции фронтали этой плоскости. Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим проекциям горизонтали h и фронтали f этой плоскости.

На изображены прямые, перпендикулярные плоскостям, заданным различными способами.

Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы.

Следовательно, прямая а перпендикулярна плоскости α, если ее проекции перпендикулярны соответствующим пересекающимся следам плоскости.