Раздел 4.Комплексные числа.

84)Алгебраическая форма комплексного числа.

Запись комплексного числа Z в виде x+iy,x,y принадлежат R называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что

i^2=-1.

86)Операция сложения комплексных чисел в алгебраической форме.

Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов; учитывая при этом, что i^2=-1;i^3=-I;i^4=i.

Суммf комплексных чисел

Правило сложения. При сложении комплексных чисел складываются действительные и мнимые части соответственно.

88)Комплексно сопряженные числа. Изображение на комплексной плоскости.

Если комплексное число z=x+iy, то число z= x-iy называется сопряжённым (или комплексно сопряжённым) к z (обозначается также z* ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

90)Тригонометрическая форма комплексного числа. Модуль и аргумент комплексного числа.

юбое комплексное число а + bi можно представить в виде:

а + bi = r (cos φ + i sin φ), (1)

где r = √a2 + b2 , а угол φ определяется из условия:

Такая форма записи комплексных чисел называется тригонометрической.

Число r в формуле (1) называется модулем, а угол φ — аргументом, комплексного числа а + bi .

Если комплексное число а + bi не равно нулю, то модуль его положителен; если же а + bi = 0, то а = b = 0 и тогда r = 0.

Модуль любого комплексного числа определен однозначно.

Если комплексное число а + bi не равно нулю, то аргумент его определяется формулами (2) однозначно с точностью до угла, кратного 2π. Если же а + bi = 0, то а = b = 0. В этом случае r = 0. Из формулы (1) легко понять, что в качестве аргумента φ в данном случае можно выбрать любой угол: ведь при любом φ

0 • (cos φ + i sin φ) = 0.

Поэтому аргумент нуля не определен.

Модуль комплексного числа r иногда обозначают | z |, а аргумент arg z. Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.

92)Операция умножения комплексных чисел в тригонометрической форме.

При умножении комплексных чисел их модули перемножаются, а аргументы складываются

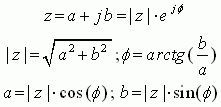
94)Операция возведения в степень комплексного числа в тригонометрической форме.

В частности, имеет место формула Муавра:

(cosj +sinj )n=cos nj +sin nj .

Если n – целое положительное число, то извлечение корня n-й степени из комплексного числа z=r(cosj+isinj ) осуществляется по формулам:

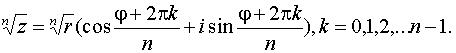
Заметим, что если положить

(это соотношение называют формулой Эйлера), то приходим к показательной форме записи комплексного числа

z=reij .

Как легко проверить, для eij выполняются правила операций со степенями, и тогда формулы умножения, возведения в натуральную степень и извлечения корня приобретают вид:

n – целое;

– целое положительное число, k=0,1,..., n–1.