Ответы на четные вопросы.

Раздел 1.Векторная алгебра.

2)Определение линейной зависимости векторов.

Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно Ai , т.е. .

4)Теоремы о линейной зависимости векторов.

Теорема1. Система векторов из R в степени n линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов из R в степени n линейно выражается через остальные векторы системы.

Теорема2. Cистема векторов из Rn линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются компоненты векторов системы:

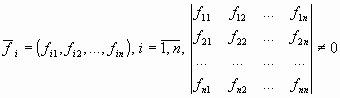
Теорема3.Два вектора линейно зависимы,тогда и только тогда,когда коллинеарны.

Теорема4.Три вектора линейно зависимы тогда и только тогда, когда они комплонарны.

6)Декартова система координат.

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

8)Геометрический смысл координат вектора.

единствен-

ности разложения имеем: .

10)Геометрический смысл линейной зависимости 3-х векторов.

а)Если есть один нулевой вектор, тогда в соответствии с теоремой о линейной зависимости, вектора а, в, с линейно зависимы.

б)Если среди векторов а, в, с – 2 вектора коллинеарны, то тогда в соответствии с теоремой они линейно зависимы, если добавить 3 вектор, то система векторов будет линейно зависимой.

в)Если среди векторов а, в, с не 0 и не коллинеарны, то приведем 3 вектора к 1 началу.

12)Скалярное произведение векторов. Определение.

Скалярным произведением в векторном пространстве над полем называется функция для элементов , принимающая значения в , определенная для каждой пары элементов и удовлетворяющая следующим условиям:

для любых трех элементов и пространства и любых чисел справедливо равенство (линейность скалярного произведения по первому аргументу);

для любых и справедливо равенство , где черта означает комплексное сопряжение (эрмитова симметричность);

для любого имеем , причем только при (положительная определенность скалярного произведения).

Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.

Заметим, что из п.2 определения следует, что . Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.